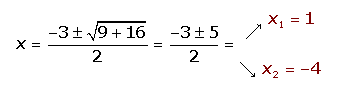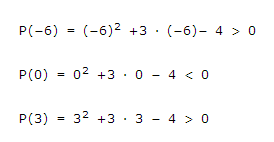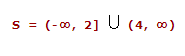Inecuaciones

Hoy vamos a estudiar las inecuaciones, como se nombre nos indica es un tipo de ecuación, con una única diferencia, que en lugar de separar el primer y segundo miembro por medio de un igual lo hace por medio de los signos de las desigualdades: o ≥ . Y cuya solución viene dada en forma de intervalo.

Por tanto, veremos inecuaciones de primer grado, inecuaciones de segundo grado e inecuaciones racionales.

CASO 1: Inecuaciones de primer grado.

Para resolver inecuaciones de primer grado, procederemos de forma análoga a la resolución de ecuaciones:

1º. Si hay denominadores, paréntesis o corchetes, se opera con ellos.

2º. Pasamos a un miembro los términos con x y al otro los términos independientes.

3º. Despejamos x, con una pequeña peculiaridad; si para despejar x es necesario pasar un número negativo dividiendo al otro lado, tenemos que darle la vuelta al signo de la desigualdad. También podemos multiplicar toda la ecuación por menos uno (-1) para que la x quede positiva, lo cual también cambiará el signo de la desigualdad.

4º. Por último expresamos la solución en forma de intervalo y representándolo en la recta real.

Ejemplo: Realiza la siguiente inecuación expresando la solución como intervalo y mediante la representación: -5(x-2) ≤ 2-x

1º. En primer lugar, quitamos los paréntesis: -5x+10 ≤ -2-x

2º. Pasamos los términos con x al primer miembro, dejando en el segundo los términos independientes: -5x+x ≤ -10-2→-4x ≤ -12.

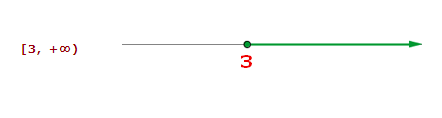
3º. Multiplicamos por -1 y cambiamos el sentido de la desigualdad: 4x ≥ 12 → x ≥ 12/4 → x ≥ 3.

4º. Solución: [3, +∞)

Observación: Recordamos que el intervalo es cerrado por un lado (es decir, semiabierto) ya que la desigualdad tiene el igual.

CASO 2: Inecuaciones de segundo grado

Para resolver inecuacioens de segundo grado seguiremos los siguientes pasos:

1º. Resolvemos la ecuación de segundo grado obtenida, haciendo caso omiso a la desigualdad. Llamemos a las raíces a y b.

2º. A continuación, representamos estos valores en la recta real, elegimos un número más pequeño que a, un número entre media de a y b, y por último un número mayor que b.

3º. Sustituimos estos valores en la ecuación inicial y anotamos el signo obtenido (+ o – )

4º. Por último, elegimos el intervalo que será nuestra solución dependiendo del signo de la desigualdad. Si tenemos > o ≥ nos está pidiendo las soluciones que nos den mayor o mayor o igual a cero, por tanto cogeremos los intervalos positivos (+). En el caso contrario, cogeremos los negativos.

Ejemplo: Resuelve la siguiente inecuación:

1º. Como ya está igualada a cero, despejamos directamente obteniendo por soluciones a=-4 y b=1.

2º. Colocamos la recta real.

3º. Sustituimos por un valor más pequeño que -4, x=-6; un número entre medias, x=0; y un número mayor, x=3.

4º. Tenemos que elegir los intervalos que sean negativos: (-4,1)

CASO 3: Inecuaciones racionales:

Las inecuaciones racionales se resuelven de forma similar a las inecuaciones de segundo grado, teniendo en cuenta que en ningún caso el denominador puede ser cero.

1º. Resolvemos por un lado la ecuación del numerador y por otro la del denominador. Supongamos que las soluciones son a y b.

2º. Representamos estos valores en la recta real.

3º. De forma análoga al caso anterior, sustituimos por un número más pequeño que a, un número entre media de los dos y un número mayor y anotamos el signo obtenido.

4º. Elegimos nuestra solución:

Ejemplo: Resuelve la siguiente inecuación: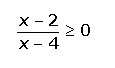

1º. Hallamos las raíces del numerado y denominador:

x-2=0 → x =2 x-4=0 → x = 4

2º. Representamos en la recta real, teniendo en cuenta que el 4, tiene que ser un punto abierto porque el denominador no se puede anular:

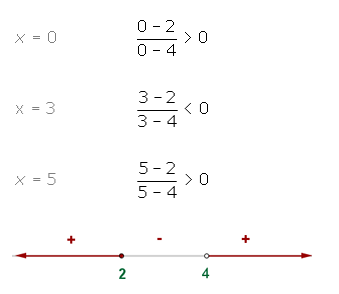
3º. Tomamos valores y sustituimos:

4º. Nuestra solución serán los intervalos positivos: