Ecuaciones con denominadores
Solucionar o resolver una ecuación implica hallar el valor de la incógnita, lo cual verificará la igualdad algebraica. Las ecuaciones más complejas requerirán del uso de técnicas determinadas. En una ecuación debemos hacer las operaciones necesarias para conservar siempre la igualdad original, por lo tanto es imprescindible la existencia de signo “=”. A continuación veremos paso por paso cómo resolver ecuaciones con denominadores, un tipo de ecuaciones que puede parecer complicado a primera vista, pero que con la práctica y el entendimiento correcto, se vuelve una tarea sencilla.
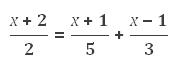
En primer lugar eliminaremos denominadores y procederemos. Para esto se multiplicarán los dos miembros por el m.c.m (mínimo común múltiplo) de los denominadores. El m.c.m es una herramienta matemática que nos permite simplificar las ecuaciones con denominadores, facilitando así la resolución de las mismas.
m.c.m (2, 5, 3) =30
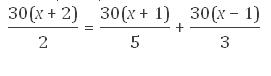
15(x + 2) = 6(x + 1) + 10(x – 1)
15x + 30 = 6x + 6 + 10x – 10
15x + 30 = 16x – 4
Luego vamos a agrupar los términos de x en un miembro y los números en el otro, nos quedará entonces de la siguiente forma:
30 = x – 4
30 + 4 = x – 4 + 4
34 = x
Luego despejamos x:
x=34
Este proceso de agrupar los términos de x en un miembro y los números en el otro es fundamental para resolver ecuaciones con denominadores. Es una técnica que se utiliza para simplificar la ecuación y facilitar la resolución de la misma.
Veamos otro ejemplo, en el que resolveremos la siguiente ecuación:
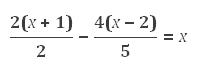
Luego simplificaremos, y nos quedará de la siguiente forma:
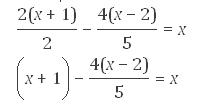
Ahora eliminamos el denominador el cual queda entonces multiplicado por cinco ambos miembros, veamos el ejemplo:
5(x + 1) – 4(x – 2) = 5x
Luego eliminamos los paréntesis:
5x + 5 – 4x + 8 = 5x
x + 5 + 8 = 5x
x + 13 = 5x
Agrupamos así, las x en un solo miembro:
13=4x
Como último paso despejamos la x dividiendo entre 4, comprobando así la solución sustituyendo el valor de x en la ecuación.
Resolver ecuaciones con denominadores es una habilidad matemática importante que se utiliza en muchas áreas de la matemática y la física. Con la práctica y el entendimiento correcto, se puede dominar esta técnica y utilizarla para resolver problemas más complejos. Es importante recordar siempre verificar la solución sustituyendo el valor de la incógnita en la ecuación original para asegurarse de que la solución es correcta.
