Progresiones aritméticas

Las progresiones no son más que sucesiones (pensar en una lista), en este caso, de números que siguen una determinada regla a la hora de aparecer representados . Esa regla, se llama diferencia y se denota como d; esta d va a ser lo que nos permita saber cuáles serán los siguientes elementos de la sucesión. Veamos un ejemplo de sucesión:

1, 3, 5, 7, 9, 11, 13, 15………

Si restamos el segundo elemento de la sucesión con el primero hallamos la diferencia, procedemos igual con los demás números:

3-1=2=d

5-3=2=d

…

15-13=2=d

Concluimos diciendo que la diferencia de la progresión es 2. Recordad que el número siguiente siempre será el número anterior más su diferencia.

Además, es importante mencionar que las progresiones aritméticas son una herramienta fundamental en muchos campos de la matemática y de la física. Por ejemplo, en la física, las progresiones aritméticas se utilizan para modelar situaciones en las que una cantidad aumenta o disminuye de manera constante. En la matemática financiera, las progresiones aritméticas se utilizan para calcular intereses, amortizaciones de préstamos y otros conceptos similares.

>>Termino general de una progresión aritmética:

Una progresión aritmética está formada por un conjunto de números, cada uno de ellos, ocupa un lugar, si los números los detonásemos con la letra «a», escrito de forma general nos quedaría algo así:

a1, a2, a3, a3, a4, a5…………an

«an» es el llamado término general, y se puede hallar de la siguiente forma:

Siendo «n» el número de posición que ocupa el último miembro de la progresión, d la diferencia de ésta y a1 y an, el primer y último miembro de la sucesión respectivamente.

Además, es interesante destacar que el término general de una progresión aritmética puede ser utilizado para resolver una variedad de problemas matemáticos. Por ejemplo, puede ser utilizado para calcular la suma de los primeros n términos de una progresión aritmética, para determinar el término en una posición específica en la progresión, o para encontrar la posición de un término específico en la progresión.

Vamos a ver un ejemplo con la progresión anterior:

1, 3, 5, 7, 9, 11, 13, 15………

a1=1 y d=2, nosotros lo que queremos hallar es an:

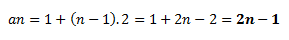
Es decir, si quisiésemos calcular cuánto valdría el número que ocupa la posición 8:

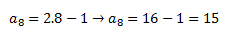
Si contáis más arriba veréis que el 15 ocupa el octavo lugar.

En el caso de que no conociésemos el valor del primer miembro, no tendríamos más que sustituir el valor de 1 por k:

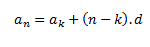
A continuación os voy a mostrar el concepto de suma en progresiones aritméticas:

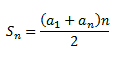
Con esto podremos saber cuántos suman los n términos de una sucesión, esto es bastante útil pues en los ejercicios os pueden mandar hallar a1 ó an y daros la suma.

Hagamos la suma de los 4 primeros términos de la progresión anterior:

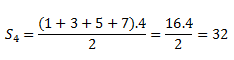
Por tanto, si sumamos los primeros 4 números de la sucesión, tendremos como resultado 32.

Os puede parecer obvio, pero, ¿Habéis pensado en el caso de que no os diesen uno de los términos? Claro, en ese caso podríamos resolverlo si conociésemos de antemano la suma de la progresión. Vamos a intentar hallar el termino x en esta sucesión:

9, 18, 27, x , 45, 54

Antes de empezar, necesitamos saber cuál es la diferencia (d):

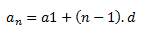
Sustituimos:

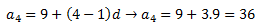
d=9

Finalmente, es importante mencionar que las progresiones aritméticas son un concepto fundamental en la matemática y su comprensión es esencial para el estudio de muchas otras áreas de esta disciplina. Por lo tanto, es importante dedicar tiempo a entender bien este concepto y a practicar con ejemplos y ejercicios para afianzar su comprensión.