Ecuaciones de primer grado

En este articulo, abordaremos la temática de las ecuaciones de primer grado, conocidas para algunos, grandes desconocidas para otros tantos. Tanto si eres del primer grupo como del segundo, no te preocupes, que aquí te lo explicamos, como siempre, en laguia2000.

Como hemos visto anteriormente, una ecuación es una igualdad que solo se verifica (se cumple) cuando las variables toman ciertos valores determinados.

Se llaman de primer grado porque los exponentes de las incógnitas ( x, y…etc.) están elevados a uno (son de grado uno).

Vamos a ver una ecuación de primer grado cualquiera:

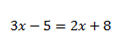
Entonces, a ambos lados de la igualdad tenemos dos simples ecuaciones, con un término independiente(un número) y después una variable con su coeficiente. Las dos variables de sendos términos, como observáis, tienen grado uno, es decir, el exponente (a lo que está elevado la equis) es uno. Esa incógnita tiene una solución que hace que ambas expresiones algebraicas sean iguales, es decir, que para un valor determinado de x esas dos ecuaciones dan lo mismo. ¿No me creéis? Pues os lo voy a demostrar:

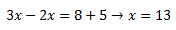
Despejando las equis a la izquierda, cambiando los signos cuando nos es necesario, y haciendo lo mismo con los términos independientes, llegamos a dar con la solución de la ecuación x= 13, lo que quiere decir que para ese valor de x, las dos ecuaciones dan lo mismo:

Si por algún casual os da distinto en un lado que en otro, es que algo habéis hecho mal.

Este es un caso sencillo, pues no tiene denominadores ni paréntesis, así que voy a generalizar la resolución de las ecuaciones de primer grado, para que sepáis resolverlas sea cual sea, y después haré un par de ejemplos para terminar de aclararlo. Vamos a ello:

Resolución general para ecuaciones de primer grado.

1º Primero quitamos los paréntesis.

2º Después quitaríamos los denominadores, en caso de que los hubiese.

3º Agrupamos los miembros que tengan x en un lado y los que no, en el otro lado de la igualdad.

4º Reduciremos los términos que sean semejantes, es decir, lo que tenga x lo sumamos o restamos con lo que tenga x y lo mismo para los términos independientes, el objetivo aquí es simplificar la ecuación lo más posible.

5º Procedemos a despejar la incógnita. Si hemos hecho bien los anteriores pasos, no deberíamos de tener problemas para la realización de éste último.

Veamos un ejemplo aplicando estos pasos, pensemos en una ecuación tal que así:

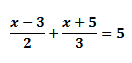
1º En este caso no hay paréntesis que quitar, así que vamos directamente al segundo.

2º Quitamos denominadores mediante mínimo común múltiplo ( mirar lección sobre ello en otro artículo):

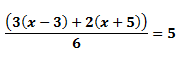
**Pista** : Un truco para realizar rápido este cálculo es multiplicar en cruz denominadores y numeradores y dividirlos por el mínimo común múltiplo de los denominadores, es decir, los números que sean comunes y los no comunes( los que se repiten y los que no) al mayor exponente.

3º Agrupamos los miembros que tengan equis a un lado de la igualdad y en el otro lado ponemos los demás (el 30 sale de hacer 6*5 =30, el denominador pasa multiplicando al otro lado de la igualdad)

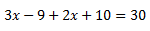
4º Reducimos los términos con x y los independientes también, por supuesto.

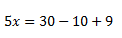
5º Despejamos la incógnita.

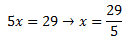
Una vez que hemos resuelto la ecuación, es importante verificar que la solución es correcta. Para ello, simplemente sustituimos la solución en la ecuación original y comprobamos que se cumple la igualdad. Si la igualdad se cumple, entonces nuestra solución es correcta. Si no se cumple, entonces hemos cometido un error en algún punto del proceso de resolución.

Las ecuaciones de primer grado son fundamentales en muchas áreas de la matemática y de la ciencia en general. Se utilizan en física, química, economía, ingeniería, entre otras disciplinas. Por lo tanto, es esencial tener una buena comprensión de cómo resolver este tipo de ecuaciones.

Además, las ecuaciones de primer grado son la base para entender ecuaciones de grados superiores. Por ejemplo, las ecuaciones cuadráticas, que son de segundo grado, se pueden resolver utilizando técnicas similares a las que hemos visto aquí, pero con algunos pasos adicionales. Por lo tanto, dominar las ecuaciones de primer grado es un paso importante para poder resolver ecuaciones más complejas.

Esperamos que este artículo te haya ayudado a entender mejor las ecuaciones de primer grado. Recuerda que la práctica es la clave para dominar cualquier concepto matemático, así que te animamos a resolver tantas ecuaciones de primer grado como puedas. ¡Buena suerte!

Y eso es todo, así termina esta lección, no olvidéis practicar unos cuantos hasta que os salgan. Nos vemos en el siguiente articulo!!