Teorema fundamental del álgebra

Para empezar, citemos el teorema:

Todo polinomio de grado n, con coeficientes complejos, tiene exactamente n raíces, no forzosamente distintas, es decir contadas con su orden de multiplicidad.

¿Qué cosa tan rara dicen verdad? Suena a chino. Vamos a desgranarlo:

Supongo que a estas alturas, seguidores fieles del blog, sabréis lo que es un polinomio. En caso contrario, ir a la lección sobre polinomios, y a refrescar la memoria se ha dicho.

Como soy muy bueno, os dejo aquí un ejemplo de polinomio, pero que no se repita otra vez eh!:

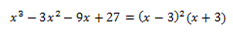
Pues ese polinomio, es real ( y complejo, pues tiene más de cuatro términos), y además, posee un total de tres raíces (soluciones), como se puede apreciar una vez simplificado, que son 3 y -3.

Generalizando:

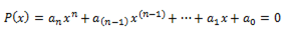
Que podemos factorizar como:

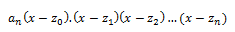
Simplemente hemos sacado factor común an y lo multiplicamos por (x-zn), siendo z = x^n.

Os voy a poner un ejemplo, para veáis la aplicación gráfica del teorema:

>> Ejemplo:

Encontrar la solución de la siguiente ecuación: y=2x+1

Para poder encontrar las soluciones reales, debemos cruzar esa recta con el eje x, esto implica hacer y=0:

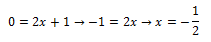
Para este caso en concreto, vemos que esta ecuación, solo tiene una única solución, -1/2.

Según el teorema, si el grado es impar, tenemos al menos una raíz real.

Para entenderlo, vamos a reescribirlo de esta manera:

Un polinomio de grado n impar admite al menos una raíz real. Si existe una raíz compleja 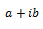de un polinomio, entonces existe su raíz compleja conjugada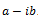

En el ejemplo anterior, era una ecuación de grado uno (mirad el exponente de las x), por lo que el número mínimo de raíces va a ser 1. Lo cual no quiere decir que tenga que haber solamente una raíz, puede haber más, pero siempre será ese mínimo.