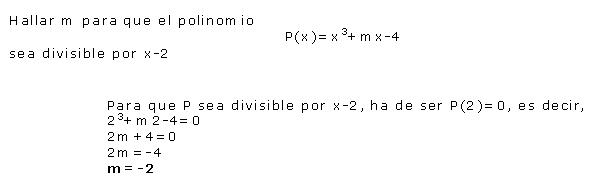Teorema del resto

El teorema del resto es un método por el cual podemos obtener el residuo de una división algebraica pero en el cual no es necesario efectuar división alguna. Nos permite de esta forma averiguar el resto de la división de un polinomio p(x) entre otro de la forma x-a por ejemplo. Se deduce de este teorema que un polinomio p(x) es divisible entre x-a sólo si a es una raíz del polinomio, únicamente si y sólo si p(a) =0.

Si C(x) es el cociente y R(x) es el resto de la división de un polinomio cualquiera p(x) entre un binomio que sería (x-a), aplicamos el algoritmo de la división:

P(x) = C(x) • (x – a) + R(x)

Entonces el valor numérico de p(x), para x=a, será igual al resto de su división entre x-a. Entonces diremos que:

P(a) = C(a) • (a – a) + R(a) = R(a)

Por ejemplo el resto de la división de un polinomio:

Entre x-2 , dará como resultado el polinomio:

Aquí vemos que esta división no es exacta y por lo tanto x-2 no es un divisor de p (x)

Observemos otro ejemplo :

Tenemos el polinomio

Al dividir p(x) entre x − 2 obtenemos el cociente :

Entonces podemos asegurar que :

En general para hallar el resto de una división entre x-a resulta mas conveniente aplicar la regla de Ruffini que sustituir la x. Por lo tanto el teorema del resto es mas adecuado para resolver problemas como el siguiente: