Teorema de Sturm
Este teorema fue desarrollado por el matemático francés Jacques Charles François Sturm (29 de septiembre de 1803 – 15 de diciembre de 1855) Tiene como principal objetivo, descubrir los ceros de una función polinómica.
Lo primero que vamos a ver para entender y razonar este tema es el sistema de polinomios del sistema. Esto es de gran importancia y necesario para hacer y formar una evaluación en la cual la cantidad de veces que se cambie de signo entre las distintas evaluaciones nos dará como resultado el número de ceros entre los valores.
Sistema de polinomios de Sturm
Supongamos entonces que queremos averiguar los ceros de un polinomio f (x), en primer lugar lo que debemos buscar al utilizar el Teorema de Sturm será un sistema de polinomios, para poder así realizar una evaluación en él. Veamos de que forma proceder.
El primer polinomio es el propio f (x); el segundo es f»(x), esto quiere decir que es la derivada del polinomio f (x), a dicho polinomio lo señalaremos como f1(x); para el tercer polinomio debemos proceder a realizar la división de f (x) entre f1(x), el residuo que se obtendrá con signo contrario será f2(x); este procedimiento seguirá siendo así, por lo cual , f3(x) va a ser el residuo con signo contrario de la división de f1(x) entre f2(x); el procedimiento finalizará cuando se obtenga como resultado una constante.
Si realizamos los cálculos sin la ayuda de una calculadora, podemos realizar los cálculos de forma en la cual no surjan fracciones en la división, tornándola más sencilla. Entonces si el dividendo es,
![]()
y el divisor es,
![]()
multiplicaremos,
![]()
Si la división es realizada por una calculadora, no es necesario multiplicar el dividendo puesto que esto no incide en el resultado del teorema. Veamos un ejemplo:
![]()
Solución,
![]()
Al efectuar la división de 3 elevado a 2 f (x) entre f1(x) obtenemos lo siguiente,
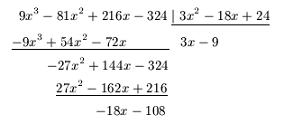
Así f2(x) = 18x + 108
Entonces hacemos la división de 18 elevado a 2 f1(x) entre f2(x) por lo cual obtenemos,

Así, f3(x) = – 77760
El sistema que se obtiene para esta función,
![]()
es el siguiente,
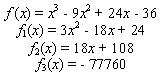
Teorema de Sturm
Siendo f (x) un polinomio de coeficientes reales tales que f (x) = 0 no adquiere raíces múltiples. Vamos ahora a llevar a cabo un sistema de Sturm para f (x). Siendo a y b reales, a < b y ninguno de ellos raíz de f (x) = 0. Por lo cual el número de raíces reales de f (x) = 0 entre a y b será igual a la diferencia que hay entre el número de variaciones de signo del sistema de Sturm f (x), f1(x), f2(x),..., fk - 1(x), fk(x) para x = b y el número de variaciones del sistema para x = a. Los términos que obtengan cero previamente deben ser descartados para contar los cambios de signo. El teorema de sturm requiere que la ecuación no tenga raíces múltiples, pero la posibilidad que hay de que una persona evalúe un polinomio de esta forma es sumamente baja, ya que este teorema actúa correctamente para muchos polinomios con raíces múltiples. Por esta razón son pocos los polinomios de raíces múltiples que fracasan.
Lo principal para aislar los ceros es examinar cuántos tenemos en total, se evalúa entonces el sistema en – ∞y + ∞, también se evalúa en x = 0 para justificar cuántos ceros positivos y negativos hay, veamos,

Como en -∞ hay 2 cambios de signo y en +∞ solamente hay uno entonces de -∞a + ∞hay 2 – 1 = 1 ceros, esto quiere decir que el polinomio solo posee un cero en I R.
Ahora, de – ∞ a 0 no hay ningún cero puesto que ambos poseen igual cantidad de cambios de signo, entonces el cero se halla de 0 a + ∞ ya que al realizar la sustracción de cambios de signo se logra 2 – 1 = 1. Podemos ahora evaluar cada uno comenzando desde 0 hasta hallar en qué intervalo está.

De esto ya tenemos el conocimiento de que el cero está entre 5 y 6. En tal caso caso se encontró claramente que f (6) = 0, o sea que el único cero que posee el polinomio es x = 6. Si el cero no se hubiera encontrado directamente, se tendría que haber realizado otro procedimiento.
