Teorema de Bolzano

El teorema de Bolzano es uno de los teoremas más importantes del cálculo matemático.

ENUNCIADO:

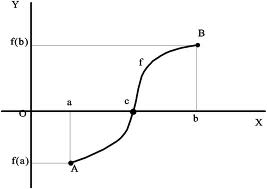
Dada una función f(x) continua en un intervalo [a,b], de tal forma que toma valores opuestos en sus extremos, es decir, f(a)0) y f(b)>0 (análogamente f(b)<0), entonces, podemos afirmar que existe un valor c dentro del intervalo abierto (a, b) tal que la función corta el eje de abscisas en ese punto: f(c)=0.

Observación: Que tengan signos opuestos en los extremos también equivale a decir que el producto de ambos tiene que ser negativo: f(a)f(b)<0

INTERPRETACIÓN GRÁFICA

Si analizamos gráficamente el enunciado del Teorema de Bolzano, podemos decir, que para toda función continua en un intervalo [a,b], tal que f(a)f(b)<0 entonces existe al menos una raíz para esa función dentro de ese intervalo: c.

APLICACIONES DEL TEOREMA DE BOLZANO

-Aproximación de raíces.

Debido a su interpretación gráfica, la principal aplicación del teorema de Bolzano es encontrar raíces o ceros de una función continua por aproximaciones. Los pasos que hay que realizar son los siguientes:

1º. Si no nos dan el intervalo [a,b] en el cual se cumple que f(a)f(b)<0, tendríamos que buscar tanteando, dos valores a y b que cumplan nuestra condición. Para que sea más fácil hacer la explicación, supongamos que f(a)0.

2º. A continuación, cogemos el punto medio del intervalo c=(a+b)/2. Si f(x)=0 ya tendríamos nuestra raíz. En caso contrario tiene que ser f(c)0, supongamos que f(c)<0, en ese caso, llamamos a´=c, y podemos decir que existe un intervalo [a´,b] donde se cumplen las condiciones del teorema de Bolzano, y por tanto, existe una raíz de la función.

3º. A partir del intervalo [a´,b] repetiríamos el paso 2, de tal forma que cada vez obtenemos intervalos más pequeños hasta alcanzar el valor de la raíz o la aproximación deseada.

Ampliación de la aplicación en la aproximación de raíces

Es importante destacar que este método, aunque sencillo, puede ser lento si la función tiene una raíz que no es fácil de encontrar. En estos casos, se pueden utilizar variantes del método de Bolzano, como el método de la bisección, que es más eficiente.

Además, el teorema de Bolzano también es útil en la resolución de ecuaciones no lineales. En este caso, si la función es continua en un intervalo [a,b] y toma valores de signo opuesto en los extremos, entonces la ecuación tiene al menos una solución en ese intervalo.

Ejemplo: Demuestra que la función, f(x)=senx-2x+3, tiene una raíz en el intervalo (1, 2). Aproxima el valor de esta raíz a las centésimas. (Para lo que utilizaremos el método anterior, teniendo en cuenta que debido a su complejidad suele realizarse con ordenador)

Para demostrar que tiene una raíz en el intervalo tenemos que estudiar si se verifica el teorema de bolzano, para ello se tiene que cumplir que:

f(x) es continua en el intervalo (1,2): lo cual se cumple ya que es continua en todos los reales.

f(1)f(2)0 y f(2)<0, también se cumple.

Por tanto podemos afirmar, que existe un c en el intervalo (1,2) tal que f(c)=0

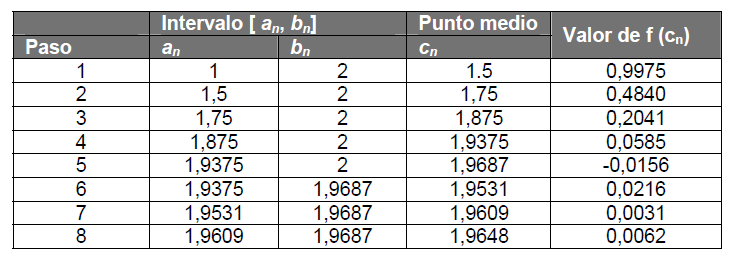
Para hallar la aproximación vamos obteniendo los valores de c realizamos los pasos anteriores, que los podemos ver en el siguiente cuadro:

Por tanto el valor de c=1,96

-Corolario de otros teoremas

Otra de las razones de la importancia de este teorema es su uso en la demostración de otros teorema del cálculo, como ocurre con el teorema de los valores intermedios:

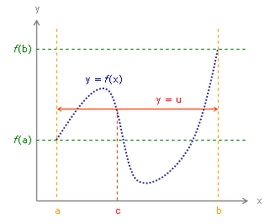
Teorema: Dada una función continua en el intervalo [a,b], entonces para cada valor de la función u, con f(a)<u<f(b), existe un punto c perteneciente al intervalo abierto (a,b), tal que f(c)=u.

Ampliación del corolario de otros teoremas

Además del teorema de los valores intermedios, el teorema de Bolzano también es fundamental en la demostración de otros teoremas fundamentales del análisis matemático, como el teorema del valor medio y el teorema fundamental del cálculo. Este último establece que toda función continua en un intervalo cerrado [a,b] tiene una antiderivada en ese intervalo, y que la integral definida de la función en ese intervalo es igual a la diferencia de los valores de la antiderivada en los extremos del intervalo.