Raíces de un polinomio

Las raíces de un polinomio son números tales que hacen que un polinomio valga cero. Podemos decir también que las raíces enteras de un polinomio de coeficientes enteros serán divisores del término independiente. Cuando resolvemos un polinomio igualandolo a cero obtenemos como soluciones las raíces del polinomio. Como propiedades de las raíces y factores de los polinomios podemos decir que los ceros o raíces de un polinomio son por los divisores del término independiente pertenecientes al polinomio. Entonces a cada raíz por ejemplo del tipo x = a le correspondería un binomio del tipo (x-a). Se puede expresar un polinomio en factores si lo escribimos como producto de todos los binomios que tengamos del tipo (x-a) que sean correspondientes a las raíces, x=a, que obtengamos. Aquí les dejo un ejemplo:

Debemos tener en cuenta que la suma de los exponentes de los binomios es igual al grado del polinomio, también tengamos en cuenta que todo polinomio que no tenga término independiente admitirá como raíz x=0, en otra forma, admitirá como factor x. Por ejemplo:

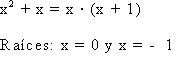
Llamaremos “primo” o “Irreducible” a un polinomio cuando no hay posibilidad de descomponerlo en factores. Observemos el siguiente ejemplo:

A continuación, les dejaré un sencillo ejercicio con su resolución :

Para adentrarnos más en el tema es necesario tener claro el teorema fundamental del álgebra, el cual fundamenta que un polinomio en una variable no constante y de coeficientes complejos, tiene tantas raíces como su grado, ya que las raíces se cuentan con sus multiplicidades. Se está afirmando con esto que cualquier ecuación algebraica de grado n posee puntualmente n soluciones complejas. Un polinomio de grado n tiene como máximo n raíces reales. Las raíces complejas de un polinomio de coeficientes reales continuamente se presentan de a pares, un polinomio de grado impar tiene mínimamente una raíz real. Hay que tener en cuenta también que un polinomio puede no poseer raíces reales. Un polinomio que tenga raíces reales y distintas es uno de los casos más simples que podemos encontrar. Por ejemplo en el siguiente polinomio en que se puede corroborar que sus raíces son, 3 ; 2 y -1.

En caso de que los coeficentes del polinomio sean complejos las raíces complejas no estarán necesariamente relacionadas. Los polinomios pueden tener entonces raíces complejas, y sus respectivas conjugadas. Por ejemplo un polinomio : Tiene una raíz compleja y su correspondiente conjugada. Para calcular una raíz compleja determinaremos su parte real, ya que la parte imaginaria, menor que cero se obtiene a partir de su módulo y de su parte real.

Sabemos que un numero “a” por ejemplo, es raíz de un polinomio P(x) si P(a) =0. Por el teorema del resto, si “a” es raíz del polinomio P(x) diremos que P(x) es divisible por x – a, ya que el resto de dividir P(x) entre x-a es cero. Generalmente a estos valores se los denomina x1, x2, x3, etc. Se aplica este teorema para verificar cual de los valores da como resto cero. El método Ruffini nos sirve también para hallar las raíces de un polinomio y así proceder a factorizar en binomios de la forma (x – a) siendo «a» un número entero.