Número algebraico
Un número algebraico es cualquier número real o complejo que sea solución de un polinomio no nulo con coeficientes racionales. En una ecuación polinómica de la forma siguiente.
![]()
![]()
Es el grado del polinomio
![]()
Los coeficientes del polinomio corresponden a números enteros.
Veamos ahora un sencillo ejemplo. Si tenemos un polinomio como,
![]()
Entonces x es algebraico, ya que el polinomio es distinto de cero, x es una raíz o 0, es decir x nos da el resultado 0 en la función. Los coeficientes son números racionales.
Si un número real o complejo no es algebraico, se denomina transcendente. Para diferenciar esto tomemos el ejemplo de la raíz cuadrada de dos, la cual es un número algebraico puesto que,
![]()
Las Propiedades de los números algebraicos son las siguientes:
Todos los números algebraicos son computables, por lo tanto son definibles.
El conjunto de los números algebraicos es numerable.
No todos los números reales son algebraicos. Los ejemplos más conocidos son π y e.
El número imaginario i es algebraico ya que es solución de,
![]()
Los números racionales son todos algebraicos. Porque toda fracción de la forma a / b es solución de bx – a = 0.
Son números algebraicos de primer grado ya que para todo número racional,![]()
una ecuación polinómica de grado uno con coeficientes enteros (qx-p=0)
cuya solución es r.
Un número irracional puede ser o no algebraico. Por ejemplo:
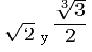
Son números algebraicos ya que son soluciones respectivamente de,
![]()
Los números irracionales no pueden ser números algebraicos de grado 1 aún si son números algebraicos.
Podemos decir también que si un número algebraico es solución de una ecuación polinómica de grado n, y no es solución de una ecuación polinómica de grado menor m 0).
Es útil y necesario tener en cuenta que la suma, diferencia, producto o cociente de dos números algebraicos da como resultado otro número algebraico.
Además de las propiedades mencionadas, es importante destacar que los números algebraicos forman un campo, lo que significa que no solo son cerrados bajo las operaciones de suma, resta, multiplicación y división, sino que también poseen una estructura algebraica rica que permite el desarrollo de teorías matemáticas avanzadas.
Una propiedad interesante de los números algebraicos es que cualquier número algebraico puede ser aproximado por números racionales con una precisión arbitraria. Esto se debe a que los números racionales son densos en el conjunto de los números reales, y por lo tanto, cualquier número real, incluyendo los algebraicos, puede ser aproximado por una secuencia de números racionales.
Otra característica notable es que los números algebraicos pueden ser clasificados según su grado. Por ejemplo, los números algebraicos de grado 1 son precisamente los números racionales. Los números algebraicos de grado 2 incluyen raíces cuadradas de números racionales que no son cuadrados perfectos, como √2 y √3. Los números algebraicos de grados superiores pueden ser raíces de polinomios más complejos.
Un aspecto fascinante de los números algebraicos es su relación con la teoría de Galois, una rama de las matemáticas que estudia las simetrías de las raíces de polinomios. La teoría de Galois proporciona una manera de entender cómo las raíces de un polinomio están relacionadas entre sí y permite determinar si un polinomio puede ser resuelto por radicales, es decir, usando únicamente operaciones aritméticas y extracción de raíces.
Finalmente, es importante mencionar que aunque los números algebraicos son numerosos y forman un conjunto infinito, los números trascendentes son aún más abundantes. De hecho, el conjunto de los números trascendentes es no numerable, lo que significa que hay «más» números trascendentes que algebraicos en el sentido de la teoría de conjuntos.
En resumen, los números algebraicos son fundamentales en la matemática y tienen aplicaciones en diversas áreas, desde la teoría de números hasta la física y la ingeniería. Su estudio no solo enriquece nuestro entendimiento de las estructuras numéricas, sino que también abre puertas a nuevas investigaciones y descubrimientos.
