Álgebra geométrica
El álgebra geométrica es un término que se aplica a la teoría de las álgebras de Clifford y teorías relacionadas. Sus elementos se denominan multivectores y se caracterizan por el producto geométrico. La teoría y propiedades de esta algebra se forman intuitiva y geométricamente, lo cual permite que sus aplicaciones en la física consigan un significado geométrico. Un multivector de grado r se denota por una letra mayúscula y es equivalente a la suma, veamos:
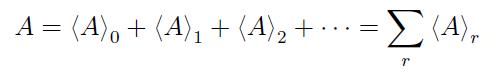
Aquí el objeto (A)r es la parte r-vector de A. Los términos como escalar, vector bivector, trivector, etc., son generalmente usados para referirse a un 0-vector, 1- vector, etc. En caso de dos vectores de dimensión n, expresados con letras minúsculas, el producto geométrico se definirá de esta forma:
![]()
a.b es el producto interno y es un escalar. Mientras que a^b es conocido como el producto externo y no es escalar ni vector es un bivector. El producto interno de dos vectores es entonces simétrico y el producto externo es antisimétrico. Por lo cual:
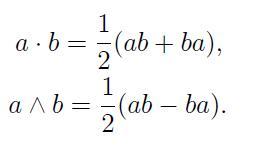
Los números reales se utilizan como escalares en un espacio vectorial V. Desde ya, un vector es algo en V mismo. El producto externo (producto exterior) se define tal que se forme el álgebra graduada (álgebra exterior de Hermann Grassmann) de Λn Vn de multivectores.
El álgebra geométrica es el álgebra que se origina por el producto geométrico (el cual es pensado como fundamental) con (para todos los multivectores A, B, C). Como característica podemos nombrar a la asociatividad, la distributividad sobre la adición de multivectores: A(B + C) = A B + A C y {A + B)C = A C + B C y La contracción para cualquier «vector» (un elemento de grado uno) a, a² es un escalar (número real).
Llamamos esta álgebra un álgebra geométrica Gn.
Lo que caracteriza a esta formulación es la correspondencia natural entre las entidades geométricas y los componentes del álgebra asociativa. La unión entre las álgebras de Clifford y las formas cuadráticas tienen origen en la propiedad de contracción. Esta pauta también da al espacio una métrica delimita por el derivado producto interno. En el algebra geométrica no hay restricción ninguna en el valor del escalar, puede suceder que sea negativa, o que sea cero (en tal caso, la posibilidad de un producto interno está eliminada si se pretende lo siguiente.
![]()
El producto escalar usual y el producto cruzado tradicional del álgebra vectorial ![]()
descubre sus lugares en el álgebra geométrica G3 como el producto interno que sería:
![]()
( es simétrico) y el producto externo es :
![]()
Con:
![]()
(Es anti simétrico). La distinción entre los vectores axiales y polares en el álgebra vectorial, es natural en álgebra geométrica como la sola distinción entre los vectores y los bivectores (elementos de grado dos). El i aquí es la unidad pseudoscalar del 3-espacio euclidiano, lo que constituye una dualidad entre los vectores y los bivectores, y se lo llama así a causa de la propiedad prevista
i² = -1.
Un ejemplo válido es R3,1, y generar G3,1, un caso del álgebra geométrica llamada álgebra del espacio-tiempo por Hestenes. El tensor del campo electromagnético, en este contexto, se convierte en simplemente un bivector E+ Ib donde la unidad imaginaria es el elemento de volumen, dando un ejemplo de la reinterpretación geométrica de los «trucos tradicionales».
Además de su aplicación en la física, el álgebra geométrica también tiene un papel importante en la informática, especialmente en la computación gráfica y la visión por computadora. En estos campos, los multivectores se utilizan para representar y manipular geometrías en tres dimensiones. Por ejemplo, en la computación gráfica, los multivectores pueden representar puntos, líneas, planos y volúmenes, y las operaciones de álgebra geométrica pueden utilizarse para calcular intersecciones, uniones y otras operaciones geométricas.
En la visión por computadora, el álgebra geométrica se utiliza para representar y manipular la geometría de la escena que se está observando. Esto puede incluir la posición y orientación de la cámara, la posición y forma de los objetos en la escena, y la relación entre diferentes puntos de vista. El álgebra geométrica proporciona un marco matemático para estas operaciones que es tanto intuitivo como eficiente computacionalmente.
En resumen, el álgebra geométrica es una herramienta matemática poderosa con aplicaciones en una amplia gama de campos. Su capacidad para representar y manipular geometrías de manera intuitiva y eficiente la hace invaluable en muchas áreas de la ciencia y la tecnología.
