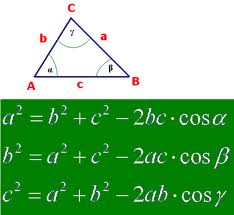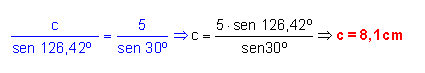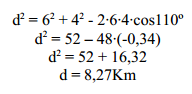Teorema del seno y del coseno
Cuando nos enfrentamos a la resolución de triángulos que no son rectángulos utilizaremos el teorema del seno o del coseno según convenga. Por tanto, vamos a estudiar cuáles son estos teoremas y cómo poder aplicarles para resolver un triángulo.
TEOREMA DEL SENO
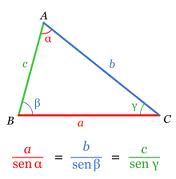
El teorema del seno nos da una razón de proporcionalidad entre los lados de un triángulo y los senos de los ángulos opuestos.
Según los datos que tengamos, utilizaremos las igualdades que nos sean necesarias.
Aplicaciones:
El teorema del seno lo utilizaremos cuando:
-Conozcamos dos ángulos y un lado opuesto a cualquiera de los dos ángulos.
-Cuando conozcamos dos lados y el ángulo opuesto a uno de ellos.
En ambos casos, podemos hallar el tercer ángulo que falta, y por tanto podemos volver aplicar el teorema del seno y terminar de resolver el triángulo.
TEOREMA DEL COSENO
El teorema del coseno se obtiene de la generalización del teorema de Pitágoras para triángulos rectángulos. El cuadrado de un lado del triángulo es igual a la suma del cuadrado de los otros dos lados menos el doble del producto de los lados por el coseno del ángulo que forman estos lados.
Dependiendo del lado que queramos calcular podemos utilizar la fórmula correspondiente:
Aplicaciones:
En algunas situaciones el teorema del seno no es suficiente para ayudarnos a resolver el triángulo que se nos plantea, estos casos son:
-Cuando conocemos los tres lados y ninguno de los ángulos, por tanto tendremos que despejar uno de los ángulos de la fórmula del teorema del coseno haciendo el arco coseno. A partir de aquí podemos utilizar el teorema del seno.
-Cuando conocemos dos lados y el ángulo que forman estos lados.
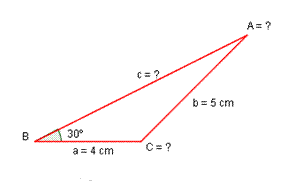
Ejemplo 1: Resolver un triángulo conocidos los siguientes datos: a= 4cm, b=5cm y que el ángulo B=30º.
En primer lugar nos centraremos en cuáles son los datos que nos han dado, para saber qué teorema tenemos que utilizar.
Conocemos dos lados y el ángulo opuesto a uno de ellos, por tanto utilizaremos el teorema del seno.
1º. En primer lugar, aplicando la primera igualdad, hallaremos el ángulo A:
2º. Una vez que ya tenemos el valor de los ángulos, calcularemos el ángulo que nos falta:
C=180-(30+23,58)=126,42º.
3º. Por último, aplicando nuevamente el teorema del seno, obtenemos el último lado.
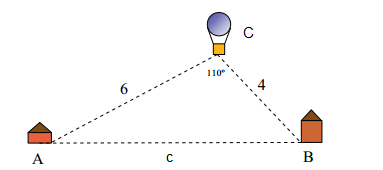
Ejemplo 2: Desde lo alto de un globo observamos el pueblo A con un ángulo de 60º y otro pueblo B con un ángulo de 50º. Si el globo se encuentra a 6 km del pueblo A y a 4 km del pueblo B, ¿a qué distancia están situados el pueblo A y B?
1º. En primer lugar, representamos la situación en la que nos encontramos mediante el siguiente triángulo, teniendo en cuenta que el ángulo que abarca el globo será la suma que nos indican 60º+50=110º, como podemos ver en la siguiente imagen:
2º. Analizamos cuáles son los datos que tenemos, en este caso conocemos dos lados y el ángulo que abarcan, por tanto aplicaremos el teorema del coseno para hallar el lado d: