Teorema de Pitágoras

Este es el famoso teorema inventado por el archiconocido Pitágoras, nacido en Crotona (Italia) en el 530 a.C. .Dicho enunciado sostenía la siguiente afirmación:

Si un triángulo cuyos lados tienen una longitud a, b y c, y dos de ellos (a y b) forman un ángulo recto (de 90º), tenemos que:

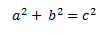
Bueno, podrá pareceros un poco abstracto, ¡Que locuras decía este Pitágoras podríais pensar! Pues no, vamos a verlo con más detalle explicando cada cosa paso a paso:

Como bien sabéis, un triángulo rectángulo es aquel que posee un ángulo recto, pues bien, el lado más grande se llama hipotenusa, y los otros dos se denominan catetos. Por tanto, la formula se podría redefinir así:

En el triangulo rectángulo, el cuadrado de la hipotenusa es igual al cuadrado de la suma de los catetos.

En la siguiente figura os muestro un triangulo rectángulo, siendo a, b y c hipotenusa y catetos respectivamente:

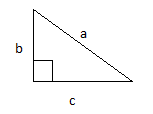
**Nota**: El cuadrado de la esquina inferior izquierda se utiliza para detonar ángulos rectos.

Bien, ahora que ya tenemos una idea de que trata el teorema, vamos a intentar demostrarlo:

Consideramos un cuadrado construido por cuatro triángulos rectángulos, de lados a, b y c, teniendo por tanto el cuadrado resultante lados cuya longitud es de a + b. Será por consiguiente su área ésta:

A= (a +b) ^2.

Pero éste cuadrado se puede dividir en los cuatro triángulos anteriores(a, b y c) mas otro cuadrado interior de lado c. Como sabemos el área de un triangulo es 1/2ab y la del cuadrado, en este caso, c^2.

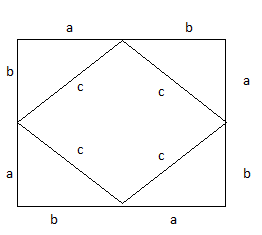
Entonces, el cuadrado grande será igual a la suma de todas las áreas, resultando:

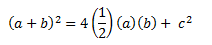
**Pista**: El 4 es porque son 4 triángulos, por tanto el área será cuatro veces la misma.

Si desarrollamos el cuadrado de una suma y multiplicando 4*1/2 = 2 nos queda:

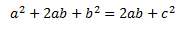
Y si restamos 2ab de ambos lados queda:

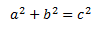
Por tanto, queda demostrada la hipótesis.

Por último querría mencionaros algunas aplicaciones para la vida cotidiana en donde se utiliza este teorema:

Si deseamos conocer la altura de un edificio conociendo cuanto mide la sombra que proyecta y la distancia del punto más alto del edificio al extremo de la sombra.

SI queremos construir una escalera para alcanzar esas manzanas que están en el árbol, podemos hacerlo sabiendo a qué altura se encuentran los frutos y la distancia del árbol a la base de la escalera.

Si nos fijamos, el ángulo que forma la escalera al apoyarse en el árbol es un triángulo rectángulo, por tanto, podemos terminar diciendo que este teorema se puede utilizar para obtener longitudes en donde intervienen triángulos rectángulos.

Además de las aplicaciones mencionadas, el teorema de Pitágoras es fundamental en diversas áreas de la ciencia y la ingeniería. Por ejemplo, en la navegación, los marineros lo utilizan para calcular distancias entre puntos en el mar. En la arquitectura, es esencial para diseñar estructuras y garantizar su estabilidad. Incluso en la informática, el teorema se aplica en algoritmos de gráficos y en el desarrollo de videojuegos para calcular distancias y trayectorias.

Otra aplicación interesante del teorema de Pitágoras es en la topografía, donde se utiliza para medir terrenos y planificar construcciones. Los topógrafos emplean el teorema para calcular distancias y ángulos en terrenos irregulares, lo que les permite crear mapas precisos y detallados.

En el ámbito de la física, el teorema de Pitágoras se usa para resolver problemas relacionados con vectores y fuerzas. Por ejemplo, cuando se analizan las fuerzas que actúan sobre un objeto en movimiento, el teorema permite descomponer estas fuerzas en componentes perpendiculares y calcular su magnitud resultante.

También es importante mencionar que el teorema de Pitágoras tiene aplicaciones en la música. Los músicos y los ingenieros de sonido lo utilizan para diseñar instrumentos y equipos de audio, asegurando que las ondas sonoras se comporten de manera predecible y armoniosa.

En la educación, el teorema de Pitágoras es una herramienta fundamental para enseñar conceptos básicos de geometría y álgebra. Los estudiantes aprenden a aplicar el teorema para resolver problemas y desarrollar habilidades de razonamiento lógico y matemático.

Finalmente, el teorema de Pitágoras tiene un papel crucial en la astronomía. Los astrónomos lo utilizan para calcular distancias entre estrellas y planetas, así como para determinar la posición de objetos celestes en el espacio. Esto les permite comprender mejor el universo y sus vastas dimensiones.

Eso es todo, nos vemos en la siguiente lección.