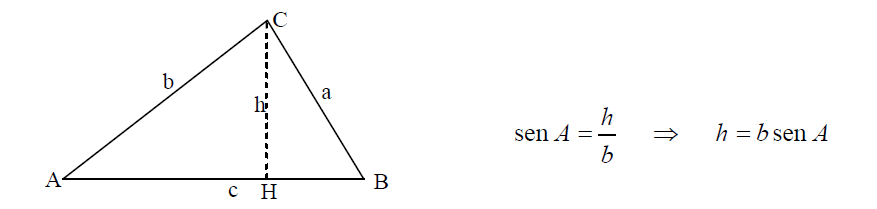
Resolución de triángulos
Resolver un triángulo es hallar las dimensiones de sus lados y la medida de sus ángulos a partir de unos datos conocidos. Vamos a ver los diferentes casos que nos podemos encontrar empezando por los diferentes tipos de triángulos que hay.
 RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
a)Conocido un lado y un ángulo (evidentemente distinto del ángulo recto):
Dependiendo de si el lado que conocemos es un cateto o una hipotenusa se resolverá de forma diferente:
● Cuando conocemos la hipotenusa a y el ángulo B:
Para hallar el ángulo que falta tendremos en cuenta que la suma de los ángulos de un triángulo tienen que sumar 180°, como uno de ellos es un triángulo rectángulo rectángulo, entonces C=90-B.
Para hallar los lados que faltan utilizaremos las razones trigonométricas(para recordarlas aquí tenéis un enlace):
sen B=cateto opuesto/hipotenusa→sen B=b/a, b=a senB
cos B=cateto contiguo/hipotenusa → cos B=c/a, c=a cosB
●Si conocemos un cateto, el b, y un ángulo B:
Para calcular el ángulo que falta procederemos de la misma manera que en el caso anterior: C=90-B. Para hallar la hipotenusa utilizaremos la razón trigonométrica del primer caso, pero despejando ahora la hipotenusa, mientras que para hallar c, utilizaremos la misma que en el anterior, aunque en cualquier caso podríamos haber utilizado el teorema de Pitágoras:
sen B=b/a, a=b/senB
cos B=c/a, c=a cosB
b)Conocidos dos lados:
Al igual que en el caso anterior también nos encontramos con dos casos diferentes dependiendo de los lados que se conozcan.
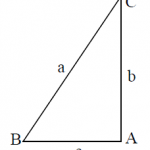
●Conocida la hipotenusa a, y uno de los catetos, b:
Para hallar uno de los ángulos utilizaremos la inversa del seno o del coseno según sea la relación que utilicemos (utilizando la que lo relaciona con el cateto contiguo o con el opuesto respectivamente). Una vez que conocemos el ángulo B, calcularemos C=90-B, y finalmente c como en los casos anteriores:
sen B = b/a → B = arcosen (b/a)
c = a cosB
● Conocidos los dos catetos b y c:
Para hallar la hipotenusa, utilizaremos el teorema de Pitágoras, una vez calculada la hipotenusa utilizaremos la fórmula del caso anterior (la del arcoseno) para hallar el B, y por último el ángulo C.
RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS
Un triángulo oblicuángulos es aquel que no es recto en ninguno de sus ángulos, en este caso, podemos abordar el problema desde dos perspectivas, una de ellas es utilizando el teorema del seno y del coseno (que veremos mañana), y la otra trazando la altura del triángulo, obteniendo de esta manera dos triángulos rectángulos:
a) Cuando el triángulo es obtusángulo:
Trazaremos su altura y calcularemos su valore, que nos servirá para resolver el resto del triángulo:
b) Cuando el triángulo es acutángulo:
Procederemos de la misma forma, obteniendo en este caso el siguiente triángulo:
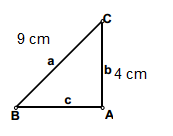
Ejemplo: Resolver el siguiente triángulo sabiendo que a=9cm y b=4cm.
Estamos en el caso en el que conocemos dos lados de un triángulo rectángulo, concretamente la hipotenusa y un cateto.
1º. Calculamos el ángulo B: senB=b/a, B=arcsen(b/a)=26,4°
2º. Calcularemos el ángulo C: C=90-26,4= 63,61º. Calculamos el ángulo B:
senB=b/a, B=arcsen(b/a)=26,4°.
3º. Por último calculamos el cateto que nos falta: c=a cos B= 8,1