Función coseno

La función coseno es una función trigonométrica, que es el resultado del cociente entre el cateto adyacente y la hipotenusa. Dicho en fórmula:

Visto así parece muy abstracto. Intentad pensar en una circunferencia, de radio uno. Como sabéis, existe la llamada circunferencia trigonométrica, que, dividiendo a ésta en cuadrantes, nos permite representar las razones trigonométricas de cualquier ángulo.

Sin entrar en mucho detalle, decir que cada uno de esos cuadrantes mide 90º, por tanto, tomaremos un ángulo rectángulo que irá girando en torno a esta circunferencia, a medida que éste rota sus valores cambian dando lugar a los distintos valores del coseno.

Mostramos a continuación el triángulo insertado en una circunferencia dividida en cuatro cuadrantes:

 

 

 

El cateto adyacente se moverá hacia la izquierda, según aumente el grado del ángulo alfa, hasta llegar a dar una vuelta completa. Si tomamos esos movimientos de la base del triangulo rectángulo, podemos formar la función coseno y ponerla en una gráfica, siendo los valores entre los que se mueve, el 1 y el -1.

La función coseno, posee diversas características que nos ayudarán a reconocerla:

 

 

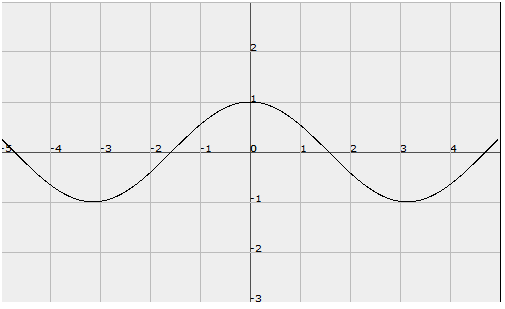
Como observáis, la curva baja y sube según el punto en donde se encuentre el cateto adyacente, ¿Qué curioso no? Si os fijáis las ondulaciones puestas juntas forman….¡Una circunferencia!!

Vamos a enumerar algunas de sus características.

Características de la función coseno:

Dominio: D(f)= R

 

Recorrido: R(f)= [−1,1]

 

Puntos de corte con los ejes:

Con el eje x: (pi/2 ,0)

Con el eje y: (0,1)

 

Simetría: par; puesto que, cos(−x )= cos(x)

 

Acotación: Donde(1< cos x <(−1))

1 es la cota superior; pues, 1 < cos x

(−1) es la cota inferior; pues, −1> cos x

 

El valor máximo es 1 y se alcanza cada 2pi veces

El valor mínimo es (−1) y se alcanza cada 2pi veces

 

La función es continua en todo su dominio

 

Es periódica, su periodo es 2pi.