Coseno de un ángulo

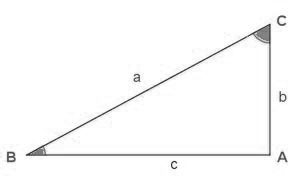
Como ya sabemos, un triángulo rectángulo tiene tres ángulos, dos de ellos agudos y uno recto. La suma de estos nos da 180 º como en cualquier triángulo. Los dos ángulos agudos suman 90. Entonces si uno de los ángulos es de A grados el otro que sería algo así como su ángulo complementario es de 90 grados. El coseno de un ángulo se define de la siguiente forma:

cos A = (lado adyacente a A)/(lado largo)

En trigonometría el coseno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto adyacente o contiguo al ángulo y la hipotenusa. Debemos tener en cuenta que el valor del coseno de un ángulo no depende de la longitud de los catetos ni de la longitud de la hipotenusa del triángulo rectángulo.

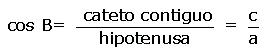
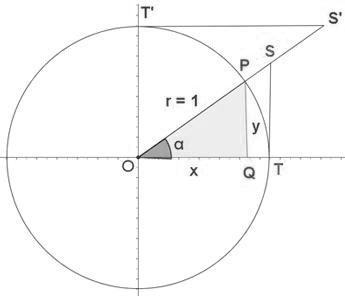
Una circunferencia goniométrica, unitaria o trigonométrica es una circunferencia de radio 1, con su centro en el origen (0,0). Esta circunferencia se utiliza con la finalidad de poder estudiar y analizar con facilidad las razones trigonométricas, por medio de la representación de triángulos rectángulos.

Observemos ahora que en una circunferencia goniométrica, el coseno de un ángulo es igual a la abscisa.

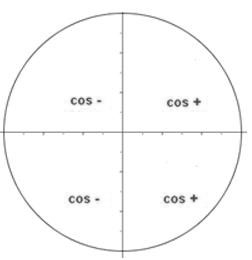
Podemos hablar del coseno de un ángulo cualquiera si utilizamos la circunferencia goniométrica, ya que esta nos permite generalizar la noción de coseno. Cualquier punto de dicha circunferencia está asociado a un ángulo “a” y si tomamos en cuenta un ángulo del primer cuadrante, el valor de coseno de tal ángulo coincidirá con la abscisa del punto, ya que la hipotenusa sería el radio, pero de valor 1. Podemos saber también mediante esta circunferencia que el valor máximo del coseno es de 1, ya que sabiendo que el coseno se mide sobre el eje x, el radio es el valor máximo que se puede obtener, por lo tanto 1 es el valor máximo del coseno. Mediante la circunferencia goniométrica también podemos identificar el signo del valor del coseno.