Seno de un ángulo

Como ya sabemos, las funciones trigonométricas nacen por el estudio del triángulo rectángulo y con la observación de las razones. Podemos decir de otro modo que surgen de los cocientes entre las longitudes de dos lados cualesquiera del triángulo, los cuales dependen del valor de sus ángulos. En este artículo veremos de cerca que es el seno de un ángulo.

Tomemos en cuenta un ángulo cualquiera de un triángulo rectángulo y denominemos a este ángulo A. Se definirá como seno del ángulo A, el cociente entre el cateto opuesto BC y la hipotenusa AC. Podría decirse también que se logra obtener el seno a partir del cociente entre la ordenada de cualquiera de los puntos del segundo lado y la distancia de este al vértice. El valor de seno está comprendido siempre entre -1 y 1.

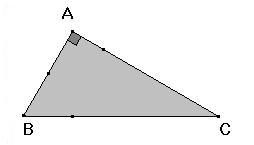
sen(B) = AC/BC

Las razones trigonométricas son válidas para todos los ángulos si utilizamos una circunferencia de radio 1 cuyo centro esté ubicado en el origen. Es importante saber que los ángulos se miden en sentido anti horario y a partir de la dirección positiva del eje de las abscisas.

Hablemos ahora de la circunferencia goniométrica, o sea aquella que tiene su centro en el origen de las coordenadas y radio 1, como ya dijimos anteriormente. Esta nos permite hacer de la noción seno algo general y de esta forma podemos hablar del seno de un ángulo cualquiera. Nos ayudará también a ver si el seno de un ángulo es negativo o positivo.

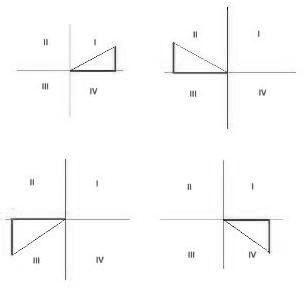
Del recuadro que se muestra mas arriba podemos sacar algunas conclusiones. El seno de cualquier ángulo en el cuadrante I, o sea un ángulo de entre 0 hasta 90 grados será positivo. En el cuadrante II, que corresponde a un ángulo de 90 a 180 grados también será positivo. En el cuadrante III el seno de un ángulo (180 ° a 270 °) es negativo. Por último en el cuadrante IV (270 ° a 360 °) es negativo.