Teorema de Rolle

El teorema del cálculo matemático que hoy vamos a estudiar se lo debemos al matemático francés Michel Rolle, quien se dedicó sobre todo al estudio de la teoría de ecuaciones encontrando diversos resultados entre los que cabe destacar nuestro tema de hoy: el teorema de Rolle, formulado en 1691.

También a él debemos la notación matemática que utilizamos actualmente para denotar la raíz enésima.

ENUNCIADO

Teorema de Rolle: Sea f(x) una función definida de la siguiente manera: f: [a,b]→R de tal forma que si se cumplen las siguientes condiciones:

a) f(x) es continua en el intervalo cerrado [a,b].

b) f(x) es derivable en el intervalo abierto (a,b).

c) La función tiene el mismo valore en los extremos del intervalo, es decir: f(a)=f(b).

Entonces, cuando se cumplen estas tres condiciones, podemos decir que existe al menos un punto c, dentro del intervalo abierto (a,b) tal que la función derivada en ese punto es cero: f»(c)=0.

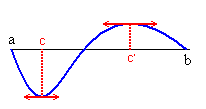
Nota: Este punto no tiene por que ser único, como podemos apreciar en las siguientes imágenes.

INTERPRETACIÓN GEOMÉTRICA

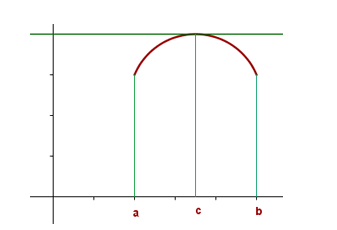
Analizando gráficamente, el teorema de Rolle quiere decir, que existirá al menos un punto (pueden ser más) del intervalo (a,b) donde la pendiente de la recta tangente en ese punto es 0 (f»(c)=0). Más concretamente, existirá al menos un valor donde la recta tangente a ese punto será paralela al eje de abscisas (OX).

Como podemos ver en las siguientes imágenes:

DEMOSTRACIÓN

Para demostrar el teorema de Rolle vamos a utilizar nociones que son conocidas y algunos nuevos conceptos para nosotros, pero que se necesitan para la demostración.

– En primer lugar, sabemos que como f es continua, la imagen de la función en el intervalo [a,b] es un conjunto conexo de R y por tanto un intervalo, el intervalo imagen.

– La imagen de la función en un conjunto compacto también es un conjunto compacto, por lo que el intervalo imagen es cerrado y acotado. Por tanto, por el teorema de Weierstrass la función alcanza su valor máximo M y mínimo en ese intervalo.

– Distingamos ahora las distintas situaciones que nos podemos encontrar:

Si el valor del máximo y el mínimo coincide: m=M, entonces significa que la función es constante, entonces el teorema se cumple para cualquier c del intervalo (a,b).

Si m≠M, supongamos que M > f(x), y por lo tanto el máximo M está alcanzado en el interior del intervalo Si c es el punto donde se alcanza, entonces f(c) = M y por definición de máximo M = f(c) ≥ f(x) para todo x de [a, b].

Considerando el cociente (f(c) – f(x)) / (c – x) es no negativo cuando x c (el denominador se vuelve negativo no nulo). Pero el límite del cociente anterior cuando x tiende a c coincide con la definición de derivada: f «(c). Por tanto el límite por la izquierda sería positivo, y por la derecha negativo: f»(c+)0. Pero la función es continua y el límite tiene que coincidir por la derecha y por la izquierda. Por tanto f»(c)=0.

Se hace de forma análoga en el caso que se alcance el mínimo.

APLICACIONES

1. Este teorema se utiliza como demostración en otros teoremas derivados. Como es el caso del teorema de Lagrange, también conocido como el teorema del Valor Medio o de los Incrementos finitos:

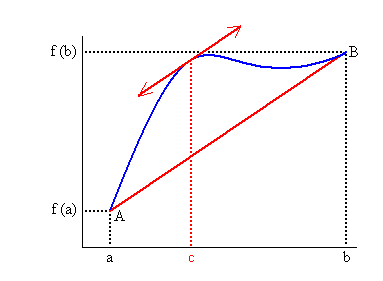
Teorema de Lagrange: Sea f(x) una función continua en el intervalo [a,b] y derivable en el intervalo abierto (a,b), entonces existe al menos un punto c en el intervalo (a,b) tal que:

f»(c)=[f(b)-f(a)]/(b-a).

Cuya interpretación geométrica es la siguiente:

2. Verificar si existe al menos un punto que verifica el teorema de Rolle en el intervalo [-1,2] de la siguiente función.

Por tanto, tenemos que comprobar que se cumplen las hipótesis del teorema:

a) f(x) es continua en el intervalo [-1,2] por tratarse de una función polinómica.

b) Por la misma razón, f(x) es derivable en el intervalo (a,b)

c) f(-1)=f(2)=0.

Por tanto, existe al menos un punto c en el intervalo (-1,2) tal que f»(c)=0.