Tangente de un ángulo
La tangente es en trigonometría una herramienta relacionada con el seno y el coseno, razones que ya hemos estudiado. Ahora veremos más de cerca que es la tangente de un ángulo. Como ya sabemos los triángulos rectángulos son básicos en el estudio de la trigonometría. La tangente de un ángulo es la razón entre la longitud del cateto opuesto del ángulo dividido entonces por el largo del lado adyacente del ángulo.
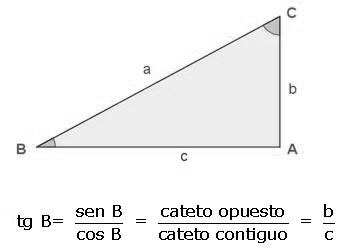
Observemos que la tangente del ángulo B es la razón entre el cateto opuesto del ángulo y el cateto inmediato al ángulo.
Debemos tener siempre en cuenta que los valores de la tangente de un ángulo así como los valores de seno y coseno dependen tan solo del ángulo y no del tamaño del triángulo. Las razones trigonométricas se pueden generalizar para cualquier tipo de ángulo, si se utiliza una circunferencia de radio 1 en cuyo centro se sitúe el origen.
Los ángulos se miden en sentido anti horario a partir de la dirección positiva del eje de las abscisas. La tangente de un ángulo es posible obtenerla si se dividen el valor de seno por el valor del coseno. En caso de tener ángulos negativos las razones trigonométricas se obtienen de igual forma, pero midiendo los ángulos en sentido horario.
Una circunferencia goniométrica sirve para medir, construir ángulos y estudiar las razones trigonométricas. Nos referimos siempre al círculo de radio 1, o podemos decir unitario. Si (x,y) es un punto en la circunferencia goniométrica y el radio forma un ángulo alfa con el eje X, las primordiales funciones trigonométricas se definen como valores de segmentos que se asocian a triángulos rectángulos auxiliares que en el caso de la tangente sería la siguiente:
![]()
Veamos a continuación una representación de los valores de las razones trigonométricas como segmentos respecto de la circunferencia unidad:
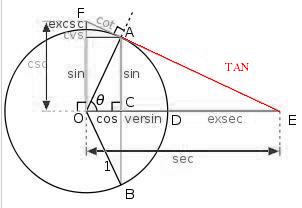
Al utilizar la circunferencia unidad, podemos saber de que signo es la tangente.
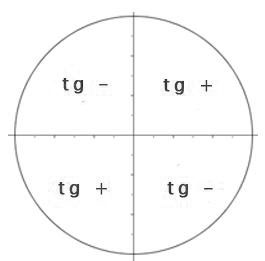
Además, es importante tener en cuenta que la tangente de un ángulo tiene algunas propiedades interesantes. Por ejemplo, la tangente de un ángulo de 45 grados es siempre igual a 1. Esto se debe a que en un triángulo rectángulo isósceles, los catetos son de igual longitud, por lo que su cociente es 1.
Por otro lado, la tangente de un ángulo de 90 grados es indefinida. Esto se debe a que el coseno de 90 grados es 0, y como la tangente se define como el seno dividido por el coseno, estaríamos dividiendo por cero, lo cual no está definido en matemáticas.
También es relevante mencionar que la tangente de un ángulo es igual a la tangente del ángulo sumado o restado 180 grados. Esto se debe a que los ángulos que difieren en 180 grados se encuentran en posiciones opuestas en la circunferencia unitaria, y por lo tanto, sus senos y cosenos son iguales en magnitud pero opuestos en signo. Como la tangente es el cociente entre el seno y el coseno, estos signos opuestos se cancelan, resultando en tangentes iguales.
Finalmente, es útil recordar que la tangente de un ángulo puede ser utilizada para resolver problemas prácticos. Por ejemplo, en física, la tangente del ángulo de inclinación de una rampa es igual al coeficiente de fricción estático entre la rampa y un objeto en reposo sobre ella. En navegación, la tangente del ángulo de elevación del sol sobre el horizonte puede ser utilizada para estimar la hora del día. Estos son solo algunos ejemplos de cómo la tangente de un ángulo puede ser aplicada en distintos campos de estudio.
