Ángulo entre dos rectas
Un ángulo entre dos rectas, por ejemplo r y s es el menor de los posibles ángulos que aparecen. Son dos ángulos, uno de ellos es agudo y el otro obtuso, a no ser que sean perpendiculares. Estos ángulos forman un vector director r con otro de s. Lo cual podemos expresar como (r, s) y estará comprendido entre 0 y π/2.
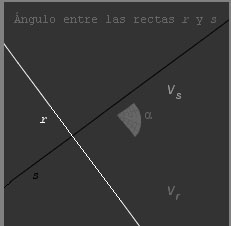
En esta imagen podemos ver representadas dos rectas y sus vectores directores. Podemos también ver claramente el ángulo que forman.
Sea (r, s) el ángulo formado por las rectas r y s. Al seleccionar los dos vectores directores vr y vs, no sabemos aún si hemos elegido los que forman un ángulo (r, s) o un ángulo π−(r, s). Aún así su producto escalar puede ser positivo si se forma un ángulo menos que π/2. O puede ser negativo si el ángulo está entre ángulo entre π/2 y π. También existe la posibilidad de que el ángulo sea nulo, si tenemos perpendiculares.
Como ya sabemos el ángulo entre dos rectas, es el menor de los ángulos que se forma de estas. Podemos obtener la medida este ángulo tanto por sus vectores directores o por sus pendientes. Veamos a continuación la representación de dos rectas y la fórmula para hallar el ángulo por sus vectores.
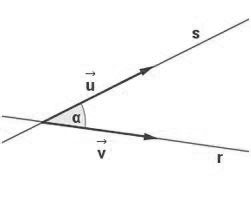
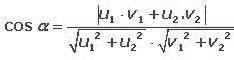
A continuación veremos un ejemplo con la fórmula anterior. Calculemos el ángulo que forman dos rectas r y s, teniendo en cuenta que sus vectores directores son :
![]()
Por lo tanto:
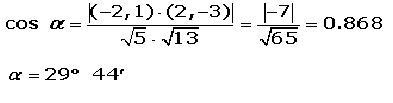
En caso de que sean perpendiculares, el producto escalar del numerador será cero y la igualdad quedará como :
![]()
Si las rectas r y s se cortan en un punto A, el cual es el vértice de un triángulo obtusángulo, Averiguaremos entonces el ángulo A de dicho triángulo. Veamos el ejemplo:
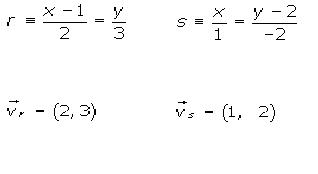
Aplicamos a continuación la fórmula:
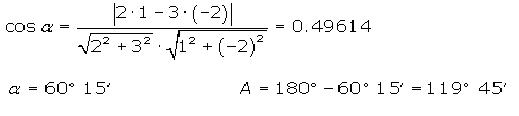
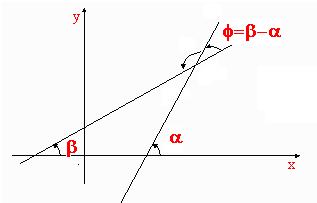
Como dijimos previamente podemos también obtener el ángulo a partir de sus pendientes. Por ejemplo dadas dos rectas con pendientes m y m’ verificaremos de la siguiente forma:
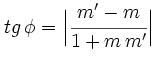
Teniendo en cuenta que :
![]()
Usaremos la fórmula de la tangente de la diferencia de los dos ángulos, por lo cual tendremos lo siguiente:
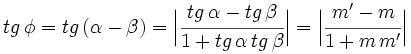
Observemos por último la siguiente representación en base a lo anterior: