Cotangente de un ángulo
La trigonometría estudia las relaciones entre los lados y los ángulos de los triángulos. Para esto utiliza las llamadas razones trigonométricas las cuales se utilizan con frecuencia en cálculos técnicos. Las funciones trigonométricas son valores sin unidades dependientes de la dimensión de un ángulo. La trigonometría es entonces el estudio de las funciones seno, coseno, tangente y sus recíprocas que serían cotangente, secante y cosecante. Esta rama de la matemática puede intervenir directa o indirectamente en las demás restantes y es aplicable a todo aquello que requiera de medidas de precisión.
Veremos hoy atentamente una de las ya dichas razones recíprocas a las razones fundamentales. En este caso la cotangente usualmente abreviada cot o cta que corresponde a la razón recíproca de la tangente o también de otra forma a su inverso multiplicativo.
![]()
La tangente y la cotangente de cualquiera de los ángulos agudos (x) de un triángulo pueden establecerse con las razones siguientes:
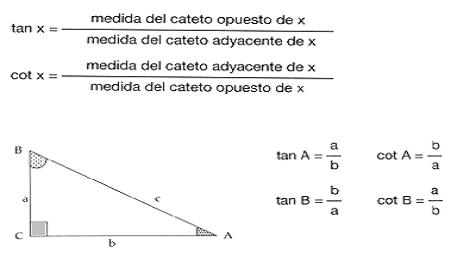
Es posible notar que las funciones trigonométricas fundamentales en relación a sus recíprocas tienen invertido sus términos. Para la función cotangente es importante tener en claro que se asocia a cada número real, x, el valor de la cotangente del ángulo cuya medida de radianes corresponde a x.
f(x) = cotg x
la variación de los valores de las funciones trigonométricas para algunos ángulos pueden representarse gráficamente. La conclusión de esto es que estas funciones son periódicas o sea que el valor de cada una se repite a intervalos regulares que se llaman periodos. El periodo de todas las funciones, exceptuado la tangente y la cotangente, es 360° o 2p radianes. La tangente y la cotangente poseen un periodo de 180 ° o p radianes. Para tener idea de lo que es un radián diremos que 1 ángulo llano = 2 ángulos rectos = 180 grados = p radianes. En matemáticas un radián es la unidad de ángulo plano igual al ángulo central establecido por un arco de longitud igual al radio del círculo. Un radián = 57,3 grados, un grado = 0,01745 radianes. Estas aproximaciones son adecuadamente exactas.
Veamos ahora los signos de la cotangente:
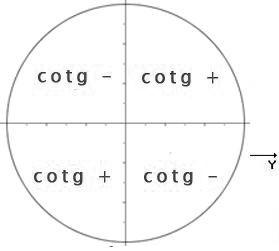
Podemos utilizar en el estudio de las funciones circulares, la circunferencia en la cual r = 1, o sea la que llamaremos circunferencia trigonométrica, de radio unidad. Esta nos permitirá hacer apreciaciones como el signo, de acuerdo con el cuadrante en que se encuentre el lado terminal de ángulo siempre teniendo en cuenta que la longitud de un punto cualquiera al origen de coordenadas es positiva siempre. Como definición de función circular diremos que cotangente circular del ángulo a”, o, simplemente, “cotangente de a” Función cotangente: f(x)= ctgx (como ya hemos dicho es inversa de la tangente)
