Cosecante de un ángulo
Como ya sabemos, la trigonometría es de la matemática, la rama que se encarga de estudiar las relaciones entre los ángulos y los lados de los triángulos. Entre las tantas aplicaciones prácticas utilizadas en trigonometría, están aquellas que determinan distancias que no se pueden medir directamente. Esto se resuelve tomando la distancia que buscamos como el lado de un triángulo y midiendo luego los lados restantes y los ángulos del triángulo. Conociendo esto se pueden utilizar las fórmulas de seno, coseno y tangente. Las funciones trigonométricas son valores sin unidades que dependen solo de la magnitud de un ángulo. Estas relaciones bastan para resolver cualquier clase de triángulo, o sea calcular los ángulos y lados desconocidos del triángulo.
Aparte de las tres relaciones básicas y fundamentales que nombramos anteriormente (coseno, seno, tangente) se encuentran otras que son las recíprocas a las anteriores y llevan el nombre de cotangente, secante y cosecante. Veremos atentamente aquí una de estas funciones que corresponde a la razón recíproca de seno o su inverso multiplicativo que llamamos cosecante y se puede abreviar como csc o cosec .
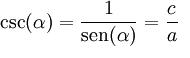
En el triángulo que se muestra a continuación podemos observar que la cosecante del ángulo B corresponde a la razón inversa del seno B. Se indica entonces por cosec B. Es posible definirlo también como el cociente del segmente orientado y la proyección vertical, o sea la hipotenusa sobre el cateto opuesto.
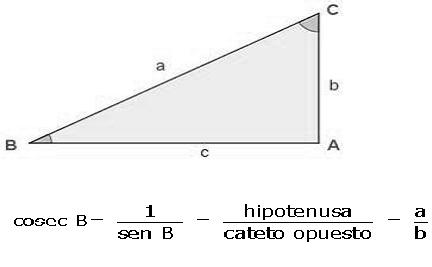
Para entrar mas en detalle de la función cosecante hablaremos de ángulos cuadrantes. De acuerdo con el cuadrante en el cual se encuentre el lado terminal de ángulo y tomando en cuenta que la distancia correspondiente a un punto cualquiera al origen de coordenadas es siempre positivo, las funciones trigonométricas pueden ser positivas o negativas, aplicando la ley de signos. Veamos ahora cual sería el signo de cosecante:
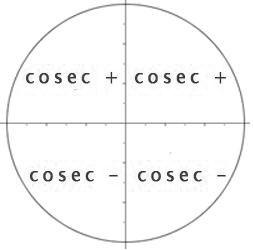
En estrecha relación con lo anterior las funciones trigonométricas circulares son aquellas que están referenciadas en la circunferencia. Usamos entonces la llamada circunferencia trigonométrica de radio unidad, para estudiar las funciones circulares . Esta nos sirve para poder observar detalladamente lo que exlicamos anteriormente, o sea el signo de la función. Observemos ahora la función cosecante y su definición como función circular:
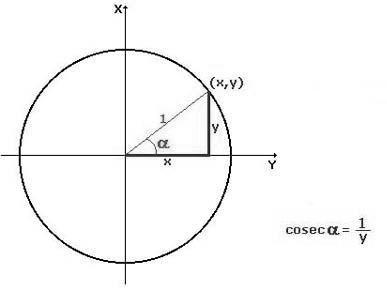
Cosecante circular de ángulo “a” o meramente cosecante de a. Función cosecante:
f(x)= cosecx (inversa del seno)
