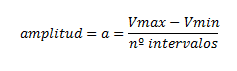Tabla de frencuencias

Una vez recogidos los datos de la muestra que vamos a estudiar es necesario agruparlos ordenándolos en forma de tabla, esta tabla recibe el nombre de distribución de frecuencia o de tabla de frecuencias.

En este apartado nos vamos a centrar en las tablas de frecuencias para variables aleatorias unidimensionales (más adelante estudiaremos las variables aleatorias bidimensionales).

Hay dos tipos de variables aleatorias:

– Las variables aleatorias discretas, que toman valores concretos. Ejemplos: el número de hermanos de una población, o el número de coches, etc.

– Las variables aleatorias continuas, que se agrupan en intervalos, ya que entre dos valores pueden haber infinitos. Ejemplos: la altura de una población, el peso, el sueldo, etc.

Además de estos dos tipos de variables, también podemos encontrar variables aleatorias mixtas, que son aquellas que pueden tomar tanto valores discretos como continuos. Ejemplos: la edad de una población, el número de hijos, etc.

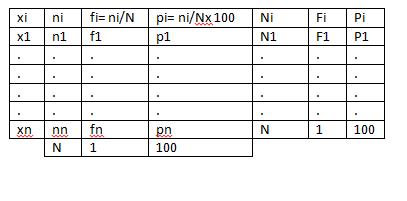
Una vez que ya conocemos los datos que vamos a representar en nuestra tabla, vamos a ver como se representan y que expresan cada uno de ellos por el orden en el que aparecen en la tabla. (La primera columna siempre estará ocupada por los datos que toma la variable aleatoria correspondiente).

– Frecuencia absoluta (ni): expresa el número de veces que aparece un determinado valor. La suma de esta columna tiene que ser igual al tamaño de la muestra (N).

– Frecuencia relativa (fi) : se calcula haciendo el cociente de la frecuencia absoluta entre el tamaño de la muestra, indica la proporción en tanto por uno de cada valor. La suma de esta columna tiene que ser igual a 1.

– Frecuencia relativa porcentual (pi): Es el porcentaje de la anterior, por tanto se obtiene multiplicando cada valor por 100. Su suma tiene que ser igual a 100.

– Frecuencia absoluta acumulada (Ni): es la suma de las frecuencias absolutas de todos los valores anteriores o iguales al considerado. Por ejemplo: N3= n1+n2+n3

– Frecuencia relativa acumulada (Fi): De forma análoga a la anterior se obtiene sumando las frecuencias relativas anteriores o iguales al valor considerado.

– Frecuencia relativa porcentual acumulada (Pi): Al igual que las anteriores se calcula sumando los valores anteriores o iguales.

De tal forma que la tabla de frecuencias quedaría de la siguiente manera:

Cuando realizamos una tabla y agrupamos los datos por intervalos debemos tener en cuenta tres condiciones:

1. El número adecuado de intervalos está entre 5 y 15, normalmente el número de intervalos es una aproximación de la raíz del tamaño de la muestra:

2. El primer valor no debe ser necesariamente el valor mínimo que toma nuestra variable, puede ser más pequeño. Al igual que le valor máximo puede ser mayor que le último valor que toma la variable.

3. La amplitud del intervalo depende de lo que se desee; si queremos que cada intervalo tenga una amplitud o si por el contrario pretendemos que todos tengan la misma. En este último caso:

Es importante mencionar que la elección de la amplitud de los intervalos puede influir en la interpretación de los datos. Si los intervalos son demasiado amplios, se pueden perder detalles importantes de la distribución de los datos. Por el contrario, si los intervalos son demasiado estrechos, la tabla puede resultar demasiado complicada y difícil de interpretar.

Aunque no sólo se pueden hacer tablas para variables, ya que también pueden representarse mediante una tabla los atributos o datos cualitativos, denominados de esta manera porque recogen cualidades de la población. Ejemplos: color de ojos de una población, géneros de películas favoritas, etc.

Ejemplo: Realizar la tabla de frecuencias del color de ojos de una clase de 20 alumnos

AZUL – MARRÓN – VERDE – VERDE – MARRÓN

MARRON – AZUL – MARRÓN – MARRÓN – VERDE

VERDE – MARRÓN – VERDE – MARRÓN – MARRÓN

VERDE – AZUL – AZUL – MARRÓN – AZUL

En el caso de los datos cualitativos, la tabla de frecuencias se realiza de la misma manera que con las variables, pero en lugar de intervalos, se utilizan las categorías de los datos. Es importante recordar que, en este caso, las categorías deben ser mutuamente excluyentes y colectivamente exhaustivas, es decir, cada individuo debe pertenecer a una y solo una categoría y todas las categorías posibles deben estar representadas en la tabla.