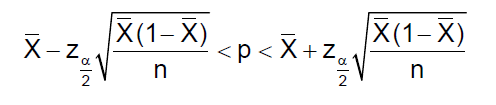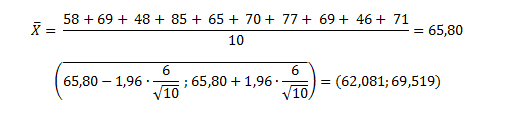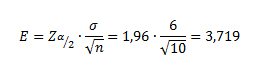Intervalos de confianza
Vamos a estudiar en esta ocasión los intervalos de confianza para la media de una población normal: µ. Daremos en primer lugar algunas definiciones generales.
DEFINICIONES:
Llamamos intervalo aleatorio (T1,T2), al intervalo cuyos extremos son variables aleatorias.
Llamamos intervalo de confianza para µ con una confianza de (1-α) al intervalo aleatorio (T1,T2) obtenido para una realización muestral dada tal que: P(T1≤ µ≤T2)=1- α.
El valor 1-α se denomina nivel de confianza, y como corresponde a una probabilidad su valor oscilará entre 0 y 1. Por otro lado el valor de α,se denomina nivel de significación.
¿PARA QUÉ UTILIZAMOS LOS INTERVALOS DE CONFIANZA?
Utilizamos los intervalos de confianza para estimar el valor de un parámetro poblacional desconocido a partir de una muestra de la población. La precisión de la estimación del parámetro dependerá de la amplitud del intervalo, es decir; a mayor amplitud menor precisión, y viceversa; a menor amplitud mayor precisión.
Centrándonos en los intervalos de confianza para la media en poblaciones normales X→N(µ;σ), donde µ es la media poblacional y σ la desviación típica poblacional. Consideremos que la media es desconocida mientras que el valor de la desviación típica es un dato conocido y que estudiamos una población de tamaño n. En estas condiciones, el intervalo de confianza para la media viene dado por la siguiente expresión:
Los niveles de confianza más utilizados normalmente son al 90%, 95% y 99%. Los intervalos de confianza para estos valores se ven reflejados en la siguiente tabla:
Ya que se trata de una estimación, nos interesa reducir el error que se pueda producir, este error viene dado por la siguiente expresión:
De esta fórmula, despejando el dato que nos interese, podemos también obtener una fórmula poder calcular el tamaño mínimo que debe tener una muestra para un cierto error cometido dado.
INTERVALOS DE CONFIANZA PARA UNA PROPORCIÓN:
Cuando en una población queremos dar una estimación de una característica que se presenta en forma de proporción (esto suele ocurrir en las poblaciones de Bernoulli), el intervalo de confianza se expresa mediante la siguiente fórmula:
Donde la media muestra se obtiene haciendo el cociente del número de éxitos entre el número total de individuos de la población.
Ejemplo: En un colegio se ha realizado un test cuya puntuación varía entre 0 y 100 puntos. Elegimos diez alumnos y alumnas al azar y anotamos sus puntuaciones: 58, 69, 48, 85, 65, 70, 77, 69, 46, 71. Sabiendo que las puntuaciones del test siguen una distribución normal y que la varianza es 36:
a) Obtener un intervalo de confianza al 95% para la puntuación media obtenida en el colegio. Explica su significado.
b) ¿Puedes determinar el error cometido? Si es así, indica su valor.
En primer lugar escribimos los datos que tenemos:
La variable aleatoria que vamos a estudiar es: X=”puntuaciones obtenidas en un colegio”
Del enunciado del problema obtenemos los siguientes dados:
La distribución de X es: X→N(µ;6).
a) El nivel de confianza: 1-α=0,95, por tanto el intervalo de confianza que tenemos que utilizar es:
Calculamos la media y sustituimos en la expresión:
Lo cual quiere decir que el verdadero valor de la media poblacional se encuentra entre 62,081 y 69,519.
b) Para calcular el error cometido que se produce al realizar la estimación, sustituimos en la fórmula anteriormente vista:
Como podemos observar nos da un error bastante grande, esto error disminuye al aumentar el tamaño de la muestra.