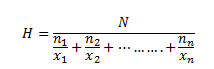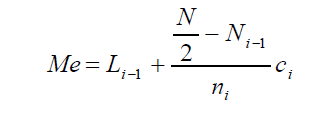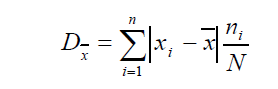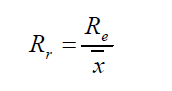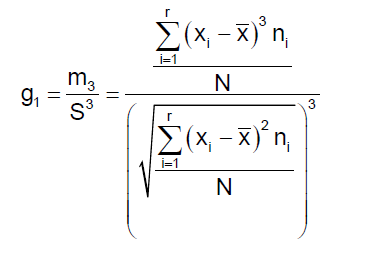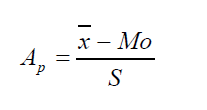Parámetros estadísticos

Para poder hacer un estudio estadístico de una característica que queremos estudiar de una población determinada, es necesario analizar una muestra de dicha población de la que podamos obtener números concretos que nos permitan analizar los datos recogidos.

Para ello utilizaremos la tabla de frecuencia que debemos elaborar con anterioridad.

Distinguimos tres tipos de parámetros estadísticos: medidas de posición, medidas de dispersión y medidas de forma.

A continuación vamos cuáles son cada una de ellas:

MEDIDAS DE POSICIÓN

Dentro de las medidas de posición distinguimos entre centrales y no centrales:

-Medidas centrales

a) Media aritmética: Como su nombre indica es el valor medio de la distribución. Se calcula mediante el cociente de la suma de todos los valores de la distribución entre el número total de datos (N):

Cuando los datos están agrupados es intervalos es necesario por tanto hallas la marca de clase:

b) Media geométrica: Se calcula haciendo la raíz n-ésima del producto de los valores que toma la distribución

c) Media armónica:

d) Mediana (Me): Es el valor que deja tanto a la izquierda como a la derecha el mismo número de frecuencias. Coincide con el cuartil 2.

e) Moda (Mo): Es el valor que tiene mayor frecuencia absoluta, es decir, el que más veces se repite.

– Medidas de posición no centrales:

a) Cuartiles: son 3 valores que dividen a la distribución en tres partes iguales

b) Deciles: son 9 valores que dividen a la distribución en 10 partes iguales

c) Percentiles: son 99 valores que dividen a la distribución en 100 partes iguales.

Por ejemplo el cuartil 1 (Q1) coincide a su vez con el percentil 25%. Y el cuartil 2 (Q2) coincide a su vez con el decil 5, el percentil 50% y la Mediana.

La fórmula para su obtención es la análoga de la mediana, cambiando N/2 por la parte que corresponda.

MEDIDAS DE DISPERSIÓN:

Estas medidas se utilizan para estudiar la representatividad de las muestras. Distinguimos entre medidas de dispersión absolutas y relativas:

-Medidas de dispersión absolutas:

a) Recorrido: Es la diferencia entre el mayor y el menos valor: R= xn – x1.

b) Recorrido intercuartílico: Es la diferencia entre el tercer cuartil y el primero Ri= Q3- Q1

c) Desviación absoluta media:

d) Varianza: mide la mayor o menos dispersión de los valores de nuestra variable respecto a la media: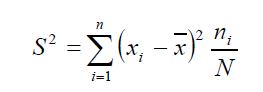

e) Desviación típica: es la raíz de la varianza.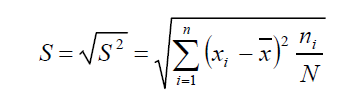

– Medida de dispersión relativas:

a) Coeficiente de apertura: es el cociente entre el mayor y el menos valor: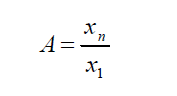

b) Recorrido relativo:

c) Coeficiente de variación de Pearson:

Cuanto mayor sea el coeficiente de variación, mayor será la dispersión y por tanto menos será la representatividad de la media.

MEDIDAS DE FORMA:

Por último, nos queda ver las medidas de forma, que se centran en el estudio de su gráfica. Las medidas de forma a su vez se clasifican en medidas de asimetría y medidas de curtosis:

-Medidas de asimetría:

Nos permite estudiar la simetría ( o asimetría) de la representación gráfica sin necesidad de llevar esta a cabo. Diremos que la distribución es simétrica si al realizar la representación gráfica y trazar una línea vertical en su media, entonces deja el mismo número de valores a ambos lados.

a) Coeficiente de Asimetría de Fisher:

Según el signo del coeficiente de asimetría distinguimos los siguientes casos:

g1=0 la distribución es simétrica.

g1>0 la distribución es asimétrica positiva.

g1<0 la distribución es asimétrica negativa

b) Coeficiente de Asimetría de Pearson: que sigue el mismo criterio de signos que el anterior.

-Medidas de apuntamiento o curtosis:

Estas medidas estudian la mayor o menos concentración de frecuencias en torno a la media. A decir verdad, lo que vamos a estudiar es la semejanza de la gráfica con la campana de gauss.

a) Coeficiente de Apertura o curtosis:

Dependiendo del signo que tenga, la distribución se llamará:

–Mesocúrtica si g2= 0,

–Leptocúrtica si g2 > 0

–Platicúrtica si g2 < 0