Sumatorio

El sumatorio no es más que una operación de suma repetida desde «n» veces (siendo n el número de sumandos) hasta infinito. Tiene muchas aplicaciones, tanto en estadística (para hallar la media, etc.) como en las series de números e incluso en integrales.

Se representa con la letra griega Σ, y se puede definir de la siguiente manera:

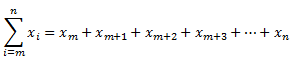
La variable i se llama índice de la suma, que nos indica cual es el primer valor inicial (desde el cual se comienza), mientras que n es el límite superior, que es hasta donde va a llegar dicha suma. Además, se tiene que cumplir que m≤n

Los sumatorios tienen unas reglas, que han de cumplirse, a la hora de realizar las operaciones. A continuación las citamos:

Regla 1: El sumatorio de una suma, es igual a la suma de las sumatorias de cada término.

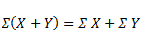
Es decir, que es lo mismo sumar primero los términos (que pueden ser datos que nos dan) y hacer luego el sumatorio, que realizarlo por separado, para cada uno de los términos.

Regla 2: La suma del producto de una constante por una variable, es igual a k veces la sumatoria de la variable.

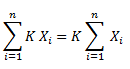
Dicho de otra forma, que si tenemos una constante K multiplicando al sumatorio, podemos sacarla para fuera (como si hiciésemos factor común, que en realidad, lo es).

Regla 3: El sumatorio de n veces una constante, es igual a N veces esa constante.

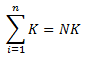
Si K es 3, sumar 3 20 veces, es lo mismo que multiplicar 3×20.

Regla 4: El sumatorio de un producto, no es igual al producto de los sumatorios de cada término.

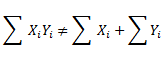
Regla 5: El sumatorio de los cuadrados de los valores de una variable, no es igual al sumatorio de la variable elevada al cuadrado.

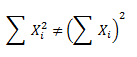
Por ejemplo, no es lo mismo sumar 1+2^2+3^2= 1+4+9 =14 que hacerlo con 1+2+3=5 y elevarlo al cuadrado, que nos daría: 25.

>>Ejemplo:

**Calcular la suma de los números impares, que se encuentran entre 14 y 4492.

Podríamos resolver este ejercicio de la forma normal, sin sumatorios, pero, es muy engorroso, pues habrá muchos números que sumar.

En lugar de eso, vamos a proceder de la siguiente forma, con sumatorios, primero planteemos la suma:

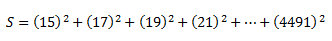
Como veis son muchísimos los impares existentes desde 15, que es el primero hasta 4491, que es el último.

Esa suma la podemos escribir también de la siguiente forma:

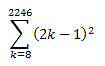
Explicación: Hemos aplicado el mismo principio que cuando tenemos una serie, y queremos sacar la expresión general de ésta. En este caso, para representar todos los números impares, escribimos 2k-1.

Los límites que hemos escogido para el sumatorio, son la mitad de la base de las potencias escritas anteriormente. Esto se hace así para que nos cuadre el resultado. Por ejemplo, veis que para k=8, si sustituimos en (2k-1)^2, nos quedaría: (2×8-1)^2=(16-1)^2= (15)^2, y así sucesivamente para los demás números.

Una vez comprendido lo anterior, vamos a desarrollar el cuadrado del sumatorio anterior:

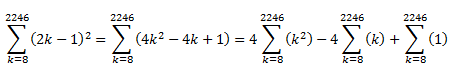
En este paso, hemos separado el sumatorio en varios, aplicando la «regla 1», y a continuación sacamos las constantes para fuera (aplicando la «regla 2»).

 

Aquí de nuevo tengo que hacer un inciso para explicar lo que pondré a continuación. Como veis hay un 4 multiplicando los 2 sumatorios, por lógica, se nos ocurriría sacar factor común de esos 2 sumatorios, pero hay un problema, el 1 se nos queda suelto, por lo que ahora el sumatorio no nos cumple la propiedad de sumar solamente los impares. para ello, hacemos un pequeño truco: cambiamos los límites del sumatorio, quedándonos esto:

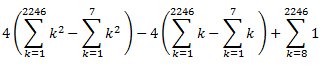
Ahora sí que podemos resolver los sumatorios uno por uno, para hallar nuestro resultado:

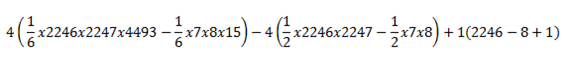
**Nota** :Acordaos que siempre se empieza por el subíndice más pequeño (el de abajo del sumatorio, en este caso, el 1 y el 8), y a continuación se ponen los demás. Como es potencia, han de ir todos multiplicando.

**Nota 2**: Para hallar el 1/6 y 1/2 se ha usado las formulas de sucesiones aritméticas, mencionadas en otro apartado.