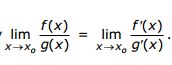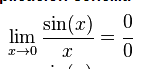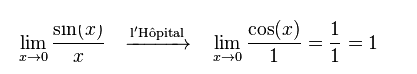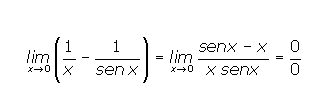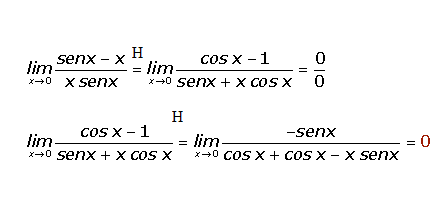Regla de L’Hôpital

En el post de hoy vamos a estudiar una regla muy usada en el cálculo matemático, la regla de L»Hôpital. La persona gracias a la que podemos usar esta regla es el matemático francés Guillaume Francois Antoine, también conocido como el marqués de L»Hôpital. L»Hôpital antes de convertirse en el matemático en el que se convirtió, inició una carrera fallida como militar. Además de ser conocido por la regla de L»Hôpital, también se conoce por haber resuelto el problema de la braquistócrona (la curva entre dos puntos de forma que se pueda recorrer en menor tiempo).

Además es autor del primer libro conocido de cálculo diferencial en el cual también incluye algunas de las explicaciones o clases de su profesor Johann Bernoulli. De ahí, que la regla de L»Hôpital también se conozca como la regla de L»Hôpital-Bernoulli.

REGLA DE L»HÔPITAL

El principal uso de la regla de L»Hôpital es la resolución de límites de indeterminación 0/0 o la de ∞/∞, mediante el uso de derivadas.

Enunciado: Sean f(x) y g(x) dos funciones continuas y derivables en un intervalo (a, b) que contiene al punto xo, de tal forma que:

-El límite de la función f(x) en el punto xo, así como el de g(x), es 0:

-La deriva de la función g(x) es distinto de cero en cualquier punto del intervalo x que sea distinto de xo: g»(x)≠0.

-Existe el límite del cociente de las derivadas respectivas en el punto xo:

Si se cumplen estas condiciones, entonces existe el límite de f(x)/g(x) y se calcula:

Observaciones:

1. Esta regla también se puede utilizar cuando la x tiende a infinito (x→∞)

2. La regla de L»Hôpital se puede aplicar tantas veces como sea necesario mientras sigan cumpliéndose las condiciones del enunciado, hasta hallar el valor del límite.

3. Esta regla también se puede aplicar para otro tipo de indeterminaciones, siempre y cuando hallamos realizado las transformaciones necesarias para convertir la indeterminación en una del tipo necesario para aplicar L»Hôpital: 0/0 o la de ∞/∞.

Ejemplo: Resuelve el siguiente límite:

En primer lugar sustituimos por el valor indicado, obteniendo una indeterminación 0/0. Por tanto, podemos aplicar la regla de L»Hôpital, derivamos numerador y denominador por separado, de tal forma que: f`(x)=cos x, g(x)=1. Entonces, el límite anterior se convierte en el siguiente límite, en el que sustituyendo obtenemos el siguiente resultado:

Ejemplo: Resuelve el siguiente límite utilizando la regla de L»Hôpital:

Al sustituir este límite, nos encontramos con una indeterminación del tipo (∞-∞). Por tanto, no podemos aplicar directamente la regla de L»Hôpital, para ello operamos (para lo que tenemos que hacer el mínimo común múltiplo):

Volviendo a sustituir obtenemos 0/0, por tanto derivamos numerador y numerador:

Y cuando volvemos a sustituir, volvemos a obtener una indeterminación, por tanto volvemos a aplicar la regla de L»Hôpital: