Máximo común divisor

El máximo común divisor es un método utilizado para la factorización de los números, es decir, para conocer cuál es el divisor más grande que esos números tienen en común (el que se repite, para entendernos) . Para hallar esto utilizaremos el método de descomposición en factores primos, existen otros, pero este es el más básico y sencillo.

-Descomposición en factores primos.

Este método se basa en descomponer, desmenuzar, un número grande en factores más pequeños, para poder ver cuáles son los que se repiten y poder conocer así cual es su máximo común divisor. Veámoslo en un ejemplo más detalladamente:

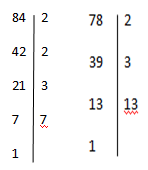
84= 2^2 x3 x7

78= 2x3x13

**Pista**: Para realizar correctamente el cálculo de arriba, debereis fijaros en el último digito del número, para ver si es par o impar, pues en ese caso dividiremos por dos o por tes. Si la suma de las dos cifras sumase impar, también sabremos que tenemos que dividir por tres o bien por un múltiplo de éste. Es importante que al final de todo os quede 1, sino, está incompleto, pues queda un factor que no habeis hallado.

Entonces, para realizar la descomposición, simplemente colocaremos una barra vertical a la izquierda del número y la extenderemos hacia abajo, según tengamos más o menos factores. En el caso anterior, el máximo común divisor sería: mcd (84, 78): 2×3=6

Por tanto, es máximo número por el que podemos dividir a 84 y 78 es 6.

La regla básica a seguir es: comunes elevados al menos exponente. Es decir, de los factores que se repitan al realizar la descomposición, escogemos tan solo los de menor exponente.

En el caso de que necesitemos hallar el máximo común divisor de tres números, podemos proceder así:

mcd(a, mcd(b,c)

Es decir, hallaríamos el máximo común divisor del primer número y el resultado de hallar el mcd para los números segundo y tercero, respectivamente.

También se puede usar para hallar el mínimo común múltiplo de otros números,, dividiendo esos dos números por su mcd:

(a.b)/mcd= mcm