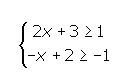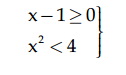Sistemas de inecuaciones con una incógnita

Como ya sabemos mucho y tenemos un gran manejo de las inecuaciones, podemos pasar al siguiente punto, los sistemas de dos inecuaciones con una incógnita (con dos incógnitas los vimos (aunque de forma particular en el caso de la programación lineal).

Este apartado no tiene ninguna dificultad, ya que los pasos para resolver un sistema de inecuaciones son casi los mismos que para resolver inecuaciones. Más concretamente, son los mismo pasos, añadiendo un paso más al final.

PASOS PARA RESOLVER SISTEMAS DE INECUACIONES

1º. En primer lugar resolvemos las inecuaciones que forman el sistema de forma separada y teniendo en cuenta del tipo que son.

2º. Representamos las soluciones de ambas inecuaciones.

3º. La solución final, será la intersección de las soluciones de las dos inecuaciones, es decir, el intervalo o intervalos donde coincidan ambas inecuaciones.

En la resolución del sistema nos podemos encontrar diferentes casos, que la solución sea un intervalo, que sea toda la recta de los números reales, o que a pesar de que las inecuaciones por separado tengan solución el sistema no lo tenga:

Ejemplo 1: Resolver el siguiente sistema de inecuaciones indicando los pasos llevados a cabo:

1º. Resolvemos las inecuaciones que forman el sistema:

1ª inecuación: 2x+3 ≥1 → 2x ≥ -2 → x ≥ -1

2ª inecuación: -x+2 ≥ -1 → -x ≥ -3 (multiplicando por menos 1 y dando la vuelta a la desigualdad) → x ≤ 2

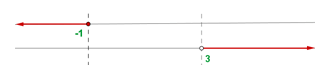
2º. Representamos la solución en la recta real:

3º. La solución del sistema, es decir, el intervalo donde coinciden ambas inecuaciones es el [-1, 3] como se puede apreciar en el paso anterior.

Ejemplo 2: Resolver, si es posible, el siguiente sistema de inecuaciones: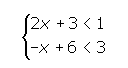

1º. Resolvemos las ecuaciones:

1ª inecuación: 2x+3 < 1 → 2x < -2 → x < -1

2ª inecuación: -x+6 < 3 → -x 3 2º. Representamos las soluciones:

3º. Como podemos observar este sistema no tiene solución, ya que la intersección es el vacío, es decir, no coinciden en ningún punto.

Ejemplo 3: Resolver el siguiente sistema con inecuaciones no lineales:

1º. El primer paso es el mismo, aunque a la hora de resolver la segunda inecuación tenemos que utilizar lo aprendido en el post anterior:

1ª inecuación: x-1 ≥ 0 → x ≥ 1

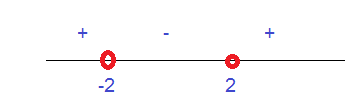
2ª inecuación: Salen como soluciones 2 y -2. Por tanto, sustituyendo en la recta real obtenemos:

Como nos interesan las soluciones negativas, nuestra solución será: (-2,2) abierto.

3º. Por último, elegimos el intervalo donde coinciden ambos: [1, 2)

Como hemos podido ver existen diferentes tipos de sistemas y soluciones que nos podemos encontrar, ¡sigue practicando!