Sistemas de inecuaciones con dos incógnitas

Ya hemos visto las inecuaciones de todos los tipos, así como algunos de los sistemas de inecuaciones con una incógnita que nos podemos encontrar, por tanto, ahora le ha llegado el turno a las inecuaciones con dos incógnitas.

Para poder resolver este tipo de sistema, antes haremos un breve estudio de las inecuaciones de dos incógnitas. Para poder resolver inecuaciones de dos incógnitas es necesario trabajar en el plano de los números reales (no solo con la recta real).

PASOS PARA RESOLVER INECUACIONES CON DOS INCÓGNITAS

1º. En primer lugar tenemos que representar la recta que se obtiene al cambiar la desigualdad de la inecuación por un igual.

Observación: Cuando en la inecuación no aparece el término en x, se trata de una recta horizontal, paralela al eje OX. Cuando sucede el caso contrario, es decir, es la incógnita y la que no aparece, se trata de una recta vertical, es decir, paralela al eje OY.

2º. La recta divide al plano en dos partes, dependiendo de la desigualdad, debemos elegir una u otra. Para ello, una forma práctica es elegir un punto del plano que no pertenezca a la recta (siempre que sea posible el (0,0) es el más fácil), sustituimos en nuestra desigualdad y, si se cumple elegimos la región del plano en la que está el punto; en caso contrario, elegimos la parte contraria.

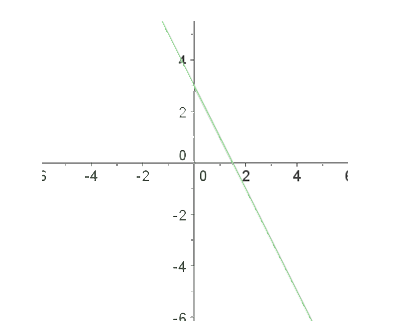
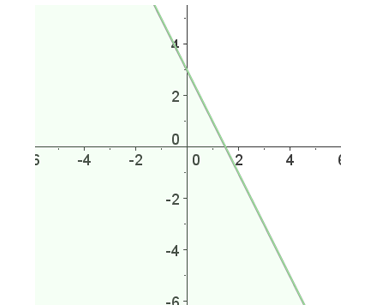
Ejemplo: Resuelve la siguiente inecuación con dos incógnitas: 2x+y ≤ 3

1º. La transformamos en una igualdad: 2x +y = 3, y realizamos una tabla de valores o simplemente damos valores para representar la recta:

-Si x=0, entonces y=3 → (0, 3)

-Si x=1, encones y=1 → (1, 1)

Representamos la recta:

2º. Elegimos una región del plano, para ello sustituimos por el punto (0,0) en la inecuación principal: 2∙0+0 ≤ 3 → 0 ≤ 3. Como el 0 es menor o igual que 3, entonces, elegimos la región donde se encuentra nuestro punto.

Esta es la solución de nuestra inecuación.

PASOS PARA RESOLVER UN SISTEMA DE INECUACIONES CON DOS INCÓGNITAS

1º. En primer lugar, de forma análoga al caso en el que solo teníamos una incógnita, resolvemos cada inecuación por separado, aunque en el mismo plano.

2º. Por último, elegimos la parte del plano donde coincidan ambas soluciones. Puede ser que no exista solución.

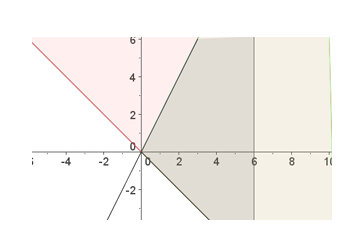
Ejemplo: Resolver el siguiente sistema de inecuaciones con dos incógnitas: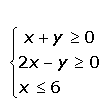

1º. Resolvemos las inecuaciones por separado:

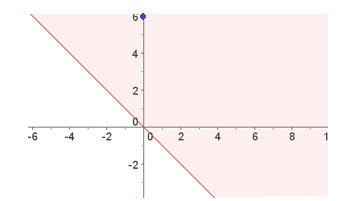
1ª inecuación: x+y ≥ 0 → x+y =0,

-Si x=0, entonces y= 0 → (0,0)

-Si x=1, entonces y= -1 → (1, -1)

Representamos la recta, y elegimos una parte. Ahora tenemos que elegir otro punto ya que el (0,0) pertenece a nuestra recta. Sea por ejemplo el (0,6), 0+6 ≥ 0 →6 ≥ 0. Como se cumple cogeremos la parte donde está el punto (0,6)

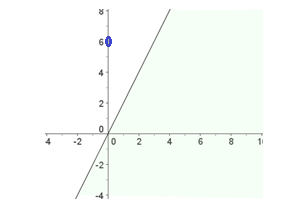
2ª inecuación: 2x-y ≥ 0 → 2x-y =0

-Si x=0, entonces y= 0 → (0,0)

-Si x=1, entonces y= 2 → (1, 2)

Elegimos, como en el caso anterior el (0,6), entonces: 2∙0-6 ≥ 0 → -6 ≥ 0. Como no se cumple, elegimos la parte contraria.

3ª inecuación: x ≤ 6 → x=6, como hemos comentado al principio, es una recta vertical, que coge todos los valores más pequeños que 6, es decir, a la izquierda del 6:

2º. Por último, nuestra solución será la parte donde coinciden todas las soluciones, será la parte que queda coloreada de un color más intenso: