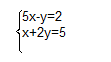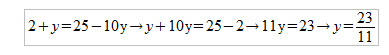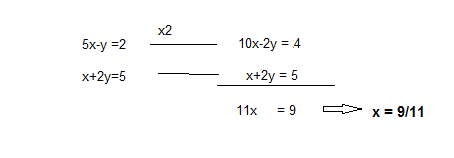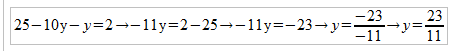Sistemas de ecuaciones lineales
Vamos a estudiar hoy los diferentes métodos que hay para resolver los sistemas de ecuaciones lineales con dos incógnitas.
Los sistemas de ecuaciones lineales son de la forma:
donde a,b,c,a´,b´y c´son números reales.
Para resolver este tipo de sistemas de ecuaciones, es decir, hallar el valor de x y de y que satisface ambas ecuaciones; podemos utilizar los métodos de igualación, reducción o sustitución que veremos a continuación.
Por tanto, veremos los pasos que hay que llevar a cabo en cada uno de ellos resolviendo un sistema como ejemplo:
MÉTODO DE IGUALACIÓN
Para resolver un sistema utilizando el método de igualación seguiremos los siguientes pasos:
1º. En primer lugar despejamos una de las incógnitas en ambas ecuaciones, es decir, o despejamos x o bien y. En este caso vamos a despejar x:
1ª ecuación: x = (2+y)/5
2ª ecuación: x= 5-2y
2º. Una vez que hemos despejado la misma incógnita en ambas ecuaciones igualamos una a la otra:
(2+y)/5=5-2y
3º. Como podemos observar nos queda una ecuación de primer grado en una de las incógnitas (en este caso la y) fácil de resolver:
4º. Una vez que ya hemos calculado una de las incógnitas, volvemos al primer paso y elegimos cualquiera de las dos ecuaciones para sustituir el valor de y, obteniendo de esta manera el valor de x. Por ejemplo utilizando la segunda ecuación:
5º. Por tanto la solución de nuestro sistema es: x = 9/11, y = 23/11.
MÉTODO DE REDUCCIÓN
El método de reducción consiste en eliminar una de las incógnitas mediante operaciones (sumas, restas y multiplicaciones) entre las ecuaciones del sistema lineal. Los pasos que llevaremos a cabo para resolver un sistema por el método de reducción son:
1º. En este caso, por ejemplo, eliminaremos la y. Para ello multiplicamos la primera ecuación por 2, y sumamos, obteniendo el valor de x.
2º. Una vez que ya tenemos una de nuestras variables ( en este caso la x), elegimos una de las dos ecuaciones donde sustituimos este valor y despejamos la otra incógnita. Por ejemplo sustituyendo en la primera tenemos:
3º. Por tanto la solución de nuestro sistema es: x = 9/11, y = 23/11.
MÉTODO DE SUSTITUCIÓN
Por último, veamos el método de sustitución, uno de los más importantes ya que los sistemas de ecuaciones no lineales muchas veces sólo podrán resolverse por este método.
Para resolver un sistema utilizando el método de sustitución llevaremos a cabo los siguientes pasos:
1º. Elegimos una de las ecuaciones donde vamos a despejar una de las incógnitas. Por ejemplo, despejamos x en la segunda ecuación:
2ªecuación: x = 5-2y
2º. Este valor se sustituye en la otra ecuación ( con la que todavía no hemos realizado ningún cálculo). En este caso lo sustituimos en la primera ecuación, quedando de la siguiente manera:
5(5-2y)-y=2
3º. Como podemos observar, se trata de una ecuación de primer grado muy simple en una de las incógnitas, que tenemos que resolver para hallar su valor:
4º. Por último, una vez que tenemos el valor de y, nos vamos al primer paso donde habíamos despejado la x, y sustituimos el valor de y:
5º. Luego la solución de nuestro problema, como era de esperar, es: x = 9/11, y = 23/11.
Aunque no lo hemos mencionado en todo el artículo, existe también un cuarto método, el método gráfico, el cual consiste en representar las ecuaciones del sistema mediante una tabla de valores, obteniendo de esta manera las rectas, y por tanto pudiendo estudiar su posición relativas.