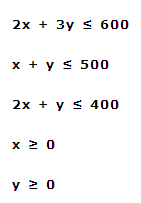Programación lineal

La programación lineal es un método para resolver problemas de optimización que están sujetos a una serie de condiciones o restricciones, las cuales vienen dadas por una serie de inecuaciones.

Para poder llevar a cabo la resolución de este tipo de problemas es necesario realizar la representación de estas restricciones en el plano, lo que dará lugar a la región factible, es decir, la región en la que se encontrará la solución a nuestra función objetivo, que es la función que tenemos que maximizar o minimizar según convenga.

Hay dos formas de poder resolver estos problemas: mediante la forma analítica o mediante la forma gráfica (menos precisa, aunque también menos trabajosa).

PASOS PARA RESOLVER UN PROBLEMA DE OPTIMIZACIÓN

A continuación veremos los pasos para llevar a cabo la resolución del problema, siendo los primeros pasos en ambos métodos es el mismo.

1º. Establecer cuáles son las incógnitas de nuestro problema.

2º. Planteamos el sistema de inecuaciones que nos dan las restricciones del problema. Cada una de las inecuaciones nos determina un semiplano del espacio, el recinto finito o infinito donde coincidan todas las restricciones será nuestra región factible. En el caso que no coincidan, el problema no tendrá solución.

3º. Escribimos la función objetivo que debemos maximizar o minimizar, (si el reciento fuese infinito sólo podríamos hallar el mínimo).

4º. Una vez que tenemos la región factible, hallamos los vértices de esta región, que serán las posibles soluciones de nuestro problema.

5º. Por el método analítico:

Comprobaremos cada uno de los vértices en la función objetivo, eligiendo el máximo o el mínimo según proceda.

Por el método gráfico:

Representamos la recta f(x,y)=0, y trazamos rectas paralelas a ella, el primer vértice del recinto por el que pase una de las paralelas será el mínimo, y el último punto será el máximo.

A continuación realizaremos un ejemplo en el podemos ver de forma concreta los pasos que se han de seguir para resolver el problema

Ejemplo: Una papelería lanza una oferta con el comienzo del curso. Para ello va a hacer dos tipos de lotes, el lote A está formado por 2 cuadernos, 1 carpeta y 2 bolígrafos, y su precio es de 6,5€. Por otro lado el lote B está formado por 3 cuadernos, 1 carpeta y 1 bolígrafo, y su precio es de 7€. Para hacer estos lotes en el almacén dispone de 600 cuadernos, 500 carpetas y 400 bolígrafos.

¿Cuántos paquetes le conviene poner de cada tipo para obtener el máximo beneficio?

1º. Elegimos las incógnitas:

x: lote A

y: lote B

2º. Planteamos el sistema de inecuaciones que nos dan las restricciones del problema (en este caso, los materiales de los que disponen en el almacén) que vienen dadas en la siguiente tabla:

Obtenemos el siguiente sistema de inecuacinoes:

3º. Escribimos la función objetivo:

f(x,y)=6,5x+7y

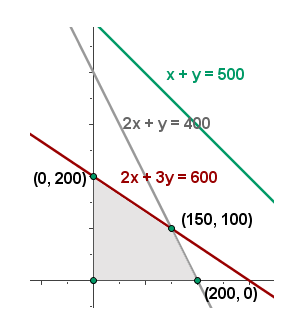
4º. Calculamos los vértices de la región factible:

5º. Realizaremos el método analítico, sustituyendo los vértices en la función objetivo:

Por tanto para obtener el máximo beneficio es necesario elaborar 150 lotes de tipo A y 100 lotes de tipo B, obteniéndose un beneficio de 1675€.