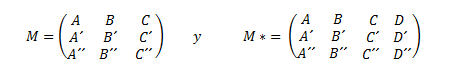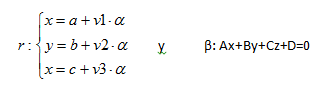Posiciones relativas de rectas y planos

Para finalizar con el estudio del espacio tridimensional, una vez vistas las distintas formas de la ecuación de una recta así como las distintas formas en que podemos encontrar la ecuación de un plano, nos faltaría estudiar su posición relativa.

Para llevar a cabo el estudio de la posición relativa de una recta y un plano podemos hacerlo utilizando las ecuaciones implícitas, estudiando las soluciones del sistema que genera; o a partir de las ecuaciones paramétricas de la recta y la implícita del plano.

Primera forma: Utilizando las ecuaciones implícitas

Dadas las recta r y el plano β en forma de ecuaciones implícitas:

Plantemos el sistema formado por las tres ecuaciones:

Obteniendo un sistema de 3 ecuaciones y 3 incógnitas.

Para hallar las posiciones relativas de la recta y el plano, vamos a discutir las posibles soluciones del sistema, para ello vamos a estudiar el rango de la matriz de los coeficientes (M) y el rango de la matriz ampliada (M*).

Nos podemos encontrar con los siguientes casos:

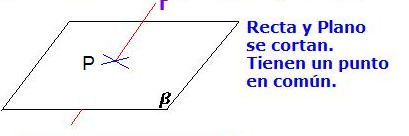
Caso1: Si rango M = rango M*=3 = nº incógnitas, entonces el sistema es compatible determinado, es decir, tiene una única solución, lo cual significa que la recta y el plano se cortan en un punto (P). Las coordenadas de este punto serán la solución del sistema.

Caso 2: Si rango M =2, rango M*=3, como los rangos no coinciden, el sistema es incompatible, es decir, no tiene solución. Lo que significa que la recta y el plano son paralelos.

Caso 3: Si rango M = 2=rango M* <3=nºincógnitas, entonces el sistema es compatible indeterminado, tiene infinitas soluciones, que geométricamente quiere decir que la recta está contenida en el plano.

Segunda forma: Utilizando las ecuaciones paramétricas de la recta y la implícita del plano

Sean dadas ahora las ecuaciones paramétricas de la recta r, que pasa por el punto P(a,b,c) y tiene por vectores v=(v1,v2,v3) ; y la ecuación implícita del plano β:

Para estudiar las posiciones relativas de la recta y el plano, sustituiremos las expresiones de la x, de la y, y de la z que nos dan las ecuaciones paramétricas en la ecuación implícita del plano, obteniendo de esta manera una ecuación con una única incógnita: α.

A la hora de resolver la ecuación nos podemos encontrar con los siguientes casos que determinarán las posiciones relativas:

Caso 1: Si la ecuación tiene solución, la recta y el plano se cortan en un punto (P), que obtendríamos sustituyendo el valor de α obtenido en la ecuación en las ecuaciones paramétricas de la recta.

Caso 2: Si la ecuación no tiene solución (0=c), entonces la recta y el plano son paralelos.

Caso 3: Si tiene infinitas soluciones ( 0=0), entonces la recta está contenida en el plano.