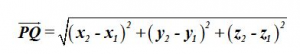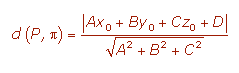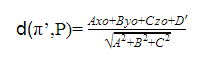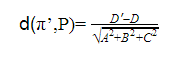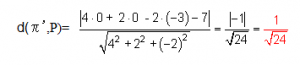Distancia entre planos paralelos

Seguimos en el campo de la Geometría y en este momento vamos a estudiar como calcular la distancia entre dos planos. Podremos calcular la distancia entre dos planos, siempre y cuando sean paralelos, ya que si fuesen secantes, la distancia entre los planos sería cero.

La distancia entre dos planos paralelos π y π» , es igual a la distancia de uno de los planos a un punto cualquiera del otro plano. Es decir sea P un punto del plano π» entonces d( π, π»)=d( π,P).

Para calcular la distancia, podemos proceder de dos formas distintas.

MÉTODO A:

Dados las ecuaciones de dos planos paralelos π: Ax+By+Cz+D=0 y π»: A»x+B»y+C»z+D»=0. Como los planos son paralelos (A,B,C)=(A»,B»,C»)

1º. Siempre en cualquier caso, tenemos que comprobar que los planos son paralelos.

2º. Hallamos un punto P del plano π».

3º. Calculamos la ecuación de la recta r perpendicular al plano π que pasa por un punto P del plano π», esta recta tendrá como vector director el vector normal al plano, es decir, v=(A,B,C).

4º. Calculamos el punto de intersección Q entre la recta r y el plano π. (Una forma fácil es escribiendo la ecuación de la recta en forma paramétrica y sustituir el valor de x, y, y z en la ecuación del plano, como mencionamos en el post anterior.

5º. Por último calculamos la distancia entre el punto P.(x1,x2,x3) y el punto Q(y1,y2,y3).

MÉTODO B:

Dadas las ecuaciones de dos planos paralelos π: Ax+By+Cz+D=0 y π»: Ax+By+Cz+D»=0. Vamos a calcular la distancia teniendo en cuenta lo dicho al principio, es decir, que la d( π, π»)=d( π,P). Por tanto, vamos a recordar que como se calculaba la distancia de un plano a un punto cualquiera del espacio.

Dado el plano π y un punto P(x1,y1,z1), la distancia entre P y π se define como al distancia del punto P a su proyección ortogonal sobre el plano π, para ello utilizamos la siguiente fórmula:

Una vez recordado lo anterior, podemos considerar la distancia entre un punto P(xo,yo,zo) del plano π, y el plano π». Por tanto, sustituyendo en la fórmula anterior obtenemos:

Teniendo en cuenta que si P es un punto π, entonces se cumple Axo+Byo+Czo=-D, por tanto sustituyendo en la ecuación anterior obtenemos la siguiente fórmula, que será la que utilizaremos de ahora en adelante:

Observación: Como la distancia no puede ser negativa, tenemos que hacer el valor absoluto de la fórmula anterior.

r último calculamos la distancia entre el punto P.(x1,x2,x3) y el punto Q(y1,y2,y3).

Ejemplo: Calcular la distancia entre el plano π: 2x+y-z-3= y el plano π»: 4x+2y-2z-7=0.

1º. Siempre tenemos que comprobar que los planos son paralelos, como el vector normal del primer plano (2,1,-1) es proporcional al del segundo (4,2,-2), entonces son paralelos.

2º. A continuación, hallamos un punto del primer plano. Para ello, damos dos valores cualesquiera a dos de las incógnitas y hallamos el valor de la tercera. Por ejemplo, si x=0, y=0, entonces, sustituyendo en la ecuación del plano obtenemos: 2∙0+0-z-3=0 →z=-3, por tanto el punto es: P(0,0,-3º. Vamos a calcular la distancia del punto P al plano π», utilizamos para ello la fórmula del segundo método: