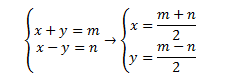Ecuaciones Diofánticas
Seguimos trabajando en la Teoría de Números, hoy le toca el turno a las ecuaciones Diofánticas, que como indica su nombre se deben a Diofanto, un antiguo matemático griego cuya obra tuvo una gran importancia e influencia en generaciones posteriores. Los problemas tratados por Diofanto se ocupaban de aspectos meramente numéricos en los que intervienen las propiedades de los números enteros.
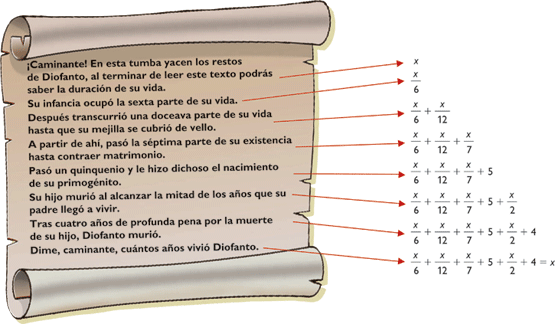
Este matemático griego además es bastante conocido debido al epitafio que se escribió en su tumba, el cual es un acertijo que a través del planteamiento de una ecuación permite conocer los años que vivió.
Dejando a un lado las curiosidades y volviendo a lo que realmente nos importa en esta ocasión, comenzaremos viendo la definición de ecuación diofántica, algunas propiedades y algunas de las ecuaciones más famosas e importantes.
DEFINICIÓN: Una ecuación diofántica es cualquier ecuación en varias variables cuyos coeficientes son números enteros y de la que únicamente nos interesan las soluciones que, a su vez, también son enteras.
Aunque también hay ecuaciones diofánticas con varias incógnitas, nosotros solo estudiaremos en este caso las ecuaciones diofánticas con dos incógnitas, tanto las lineales, como las no lineales.
ECAUCIONES DIOFÁNTICAS LINEALES
La ecuación diofántica lineal es de la forma: ax + by = c.
Llamamos ecuación lineal homogénea asociada a ella a la ecuación ax + by =0, cuya solución general viene dada por x=bk, y =-ak, para cualquier número entero k.
La ecuación diofántica lineal tendrá solución entera si y sólo si el máximo común divisor de a, b y c coincide con el máximo común divisor de a y b, es decir: M.C.D.(a,b,c)= M.C.D.(a,b).
La solución general de una ecuación lineal no homogénea se obtendrá sumando a una de las soluciones particulares, la solución general de su ecuación homogénea.
Por tanto, el problema será encontrar las soluciones particulares. Para ellos existen diversos métodos, aunque nosotros sólo vamos a ver el método de las congruencias:
Este método consiste en la aplicación del Teorema de Bezout, es decir, si d=M.C.D.(a,b), entonces existes dos números enteros p y q, tales que pa+qb=d.
La dificultad de este método es que los números p y q, suelen buscarse por tanteo. Veamos un ejemplo:
Ejemplo: Resolver la siguiente ecuación diofántica: 17x+5y =6
1º) En primer lugar compramos que esta ecuación tiene solución entera ya que:
M.C.D(17,5,6)=M.C.D.(17,5)=1
2º) Buscamos dos valores x e y tales que obtengamos un múltiplo de 17 y otro 5 cuya diferencia sea 1, 6 o cualquier divisor de 6.
x=1, y =3→17•1-5•3=2
Como el 2 es divisor de 6, si multiplicamos por 3 en ambas partes de la ecuación obtenemos:
3(17•1-5•3)=3•2→17•3-5•9=6
4º) Buscamos la solución de la ecuación homogénea: 17x+5y=0
x= 5k, y=-17k, con k un número entero cualquiera.
5º) Por tanto, la solución general de nuestra ecuación diofántica es:
(x,y)=(3,-9)+k(5,-17), para cualquier número entero k.
ECUACIONES DIOFÁNTICAS NO LINEALES
Dentro de este apartado estudiaremos los tres tipos de ecuaciones más comunes:
El método para resolver este tipo de ecuaciones es descomponer el primer miembro en producto de suma por diferencia, y el segundo como producto de dos números enteros de todas las formas posibles, a=mn, reduciendo el problema a un sistema lineal diofántico.
Una condición necesaria para que exista solución es que los factores n y m deben de tener la misma paridad.
La importancia de esta ecuación se debe, a que toda ecuación diofántica cuadrática en dos variables se puede reducir a una de este tipo.
c) Ecuaciones lineales en una de las incógnitas
Son de la forma P(x)-by=c. Que no siempre tendrán solución.
Ejemplo: Resuelve la siguiente ecuación diofántica no lineal:
El conjunto total de las soluciones se obtiene combinando los números y los signos, quedando:
(8,7); (-8,-7);(-8,7);(8,-7);(4,1);(-4,-1);(-4,1);(4,-1)