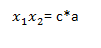Ecuaciones de segundo grado

Las ecuaciones de segundo grado, también conocidas como cuadráticas, son ecuaciones polinómicas que se pueden expresar de forma general, suponiendo una sola incógnita x y con un grado n :

 

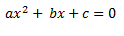
Como se puede apreciar, el grado de la ecuación es siempre dos una vez reducida la ecuación. Según falten o no algunos de sus componentes habituales, podemos clasificar las ecuaciones de segundo grado en:

 

a) Completas : Son aquellas ecuaciones formadas por todos sus componentes, y expresadas en su forma canónica, es decir:

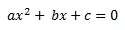
Con a, b y c distintos de cero, admite varias soluciones posibles, que veremos más adelante.

b) Incompletas puras: Son aquellas en las que los valores a y c son distintos de cero, quedándonos algo así:

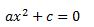
c) Incompletas mixtas: Con a y b distintos de cero, tendríamos:

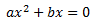
Resolución de las ecuaciones de segundo grado según sus coeficientes:

 

a)

Completas: Debemos aplicar la formula que hemos mencionado en el otro artículo, siempre se resuelven de la misma forma:

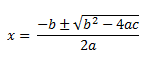
Donde (b^2 -4ac) es lo que se llama discriminante, y de su valor dependerá el numero de soluciones de la ecuación:

Hagamos un ejemplo para dejarlo todo bien claro:

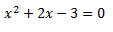
Aplicamos la formula de antes:

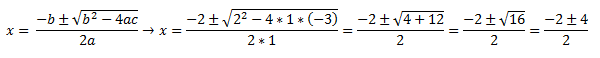
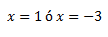
**Pista**: Recordad poner bien los signos de los coeficientes, es decir, si tiene menos ponedlo, porque como en este caso podéis ver, si no hubiese puesto el 3 en negativo, tendría una raíz negativa, y no tendría solución la ecuación, por tanto se dice que la solución es incompatible. Por lo demás esto es siempre igual, solo tenéis que aplicar la formula de arriba, es decir, que os toca memorizarla, venga, que es corta 😉

 

b) Incompletas: Según el caso, tenemos varias posibilidades para resolverlo, veamos cada una de ellas:

 

–Si c=0 , sacamos factor común y resolvemos despejando x ->

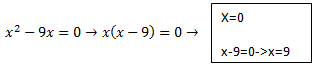
-Si b=0, pasaremos b al otro lado y efectuaremos la raíz cuadrada.

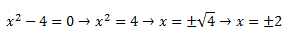
En este caso obtendremos doble solución, pues tanto -2 como 2 si se elevan al cuadrado pueden obtenerse 4.

-Si b=0 y c=0, la solución es cero:

 

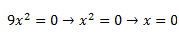
Propiedades de las soluciones de una ecuación de segundo grado:

 

a) La suma de las soluciones de las ecuaciones de segundo grado es igual al cociente de –b entre a:

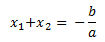
b) El producto de las soluciones de las ecuaciones de segundo grado es igual al producto de c y a: