Posiciones relativas de dos rectas
En el espacio, cuatro son las posiciones relativas que pueden adoptar dos rectas. Estas posiciones se denominan coincidentes, paralelas, secantes y rectas que se cruzan. Para comprender esto claramente supongamos que tenemos dos rectas, que serán r y s que se presentarán dadas como intersección de dos planos:
![]()
Si lo que queremos es determinar la posición referente de estas en el espacio, lo que debemos hacer es analizar el sistema que se forma por las ecuaciones de los cuatro planos cuyas matrices asociadas son las siguientes:
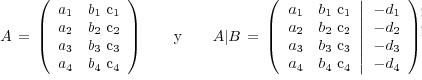
Entonces podemos decir que las dos filas primeras de A son linealmente independientes. Podemos añadir esto ya que los dos planos determinan una recta. Por lo tanto, Rango (A) y Rango ( A | B ) . Según el teorema de Rouché-Frobenius se podrán presentar a partir de esto los cuatro casos que nombramos en principio y que detallaremos a continuación:
Dos rectas pueden ser coincidentes, lo que significa que tienen todos sus puntos en común. El sistema de ecuaciones es compatible indeterminado y tiene soluciones infinitas. Rango ( A ) = Rango ( A | B ) = 2. Veamos una clara representación:
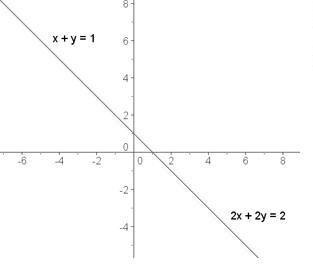
En caso de que la posición de las rectas sea paralela es sistema es incompatible y no tiene solución. Las rectas no coinciden ni se cortan en ningún punto. Pero como Rango (A) =2, las rectas son coplanarias, esto quiere decir que están en el mismo plano. Veamos un ejemplo:
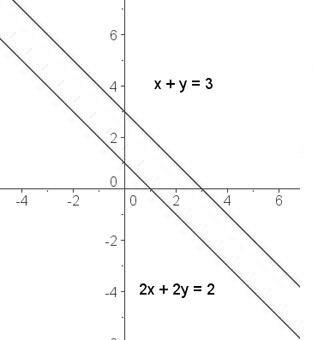
Si la posición de las rectas es secante (Rango ( A ) = Rango ( A | B ) = 3), el sistema de ecuaciones es compatible determinado y tiene una única solución. Las rectas tienen únicamente un punto en común el cual es el punto de corte. Veamos un ejemplo:
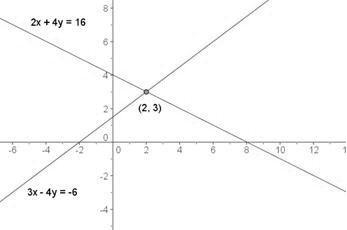
Por último tenemos las rectas que se cruzan, en lo cual el sistema es incompatible y no tiene solución. Tampoco tienen las rectas ningún punto en común y como Rango (A)=3, las rectas no son coplanarias o sea que no están contenidas en un mismo plano. Veamos:
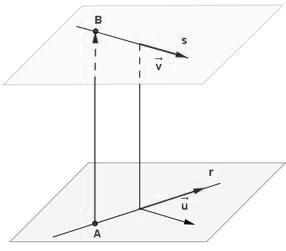
Podemos también utilizar diferentes métodos para determinar la posición relativa de dos rectas. Si obtenemos dos vectores directores u y v de cada una de las rectas, Podemos saber si estos son paralelos, ya que las rectas son coincidentes o paralelas. Para llegar a esta conclusión debemos hallar un punto en una de las rectas y comprobar si se encuentra también en la otra, de ser así las rectas son coincidentes de otro modo son paralelas. Si los vectores no son paralelos entonces las rectas son secantes o se cruzan. De ser así reuniríamos las ecuaciones de las dos rectas y procederíamos a resolver el sistema resultante. Si no tiene solución las rectas son cruzadas si tiene solución entonces son secantes.
Para profundizar en la comprensión de las posiciones relativas de dos rectas, es útil considerar la geometría tridimensional. Imagina que las dos rectas son como dos palos de madera flotando en el espacio. Si los palos se superponen completamente, son coincidentes. Si los palos nunca se tocan, pero siempre mantienen la misma distancia entre sí, son paralelos. Si los palos se tocan en un solo punto, son secantes. Y si los palos no se tocan en absoluto y no mantienen la misma distancia entre sí, se cruzan.
Además, es importante recordar que estas posiciones relativas se aplican no solo a las rectas en el espacio tridimensional, sino también a las rectas en un plano bidimensional. En un plano, sin embargo, las rectas no pueden cruzarse, ya que todas las rectas en un plano son coplanarias.
Finalmente, es importante señalar que la determinación de la posición relativa de dos rectas tiene aplicaciones prácticas en una variedad de campos, incluyendo la física, la ingeniería, la arquitectura y la informática. Por ejemplo, en la física, puede ser útil determinar si dos partículas que se mueven a lo largo de trayectorias rectas están en curso de colisión (secantes), se moverán una al lado de la otra sin colisionar (paralelas), o se moverán sin interactuar en absoluto (cruzadas).
