Posiciones relativas de planos

Vamos a estudiar hoy las distintas posiciones en las que podemos encontrar los planos en el espacio. Para ello, vamos a distinguir en primer lugar las posiciones relativas de dos planos, y a continuación, pasaremos a ampliar nuestro conjunto de planos a tres.

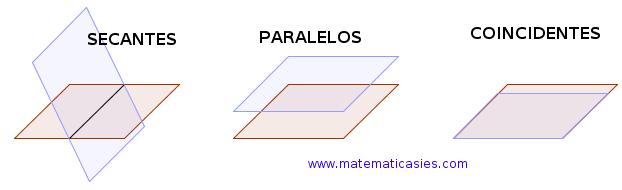
POSICIONES RELATIVAS DE DOS PLANOS

Para estudiar la posición relativas de dos planos, vamos a separar en dos casos dependiendo de los datos que conozcamos a partir de las ecuaciones (aunque ya sabemos que de todas formas siempre podemos aprendernos un único método y pasar siempre a la ecuación del plano deseada).

Caso a: Si conocemos de cada plano un punto y los dos vectores directores.

Dadas las ecuaciones de los planos en forma vectorial, paramétrica o en forma de determinante, podemos determinar un punto y dos vectores. Sea el plano π determinado por el punto P y los vectores u y v, es decir, π:{P, u, v} y el plano π»:{Q,u»,v»}.

Para conocer las posiciones relativas, estudiaremos los rangos de las matrices formadas por los vectores {u,v,u»,v»,PQ}. Recordemos que el rang{u,v}=rang{u»,v»}=2. Entonces, pueden darse los siguientes casos:

1. rang{u,v,u»,v»}=rang{u,v,u»,v»,PQ}=2, entonces los planos son coincidentes.

2. rang{u,v,u»,v»}=2 y rang{u,v,u»,v»,PQ}=3, entonces los planos son paralelos.

3. rang{u,v,u»,v»}=rang{u,v,u»,v»,PQ}=3, entonces los planos se cortan en una recta.

Observación: No tiene sentido considerar que el rango sea 4 ya que en el espacio el máximo rango es 3.

Caso b: Si los planos vienen dados por sus ecuaciones implícitas.

Sean π: Ax+By+Cz+D=0 y π»=A»x+B»y+C»z+D»=0. Para determinar las posiciones relativas de los dos planos consideraremos el sistema de 2 ecuaciones y 3 incógnitas formado por las dos ecuaciones, y estudiaremos el rango de la matriz de los coeficientes (A) y de su matriz ampliada (A|B).

1. Si rang(A)=rang(A|B)=1, entonces los planos son coincidentes.

2. Si rang(A)= 1 y rang(A|B)=2, entonces los planos son paralelos.

3. Si rang(A)=rang(A|B)=2, entonces los planos se cortan en una recta.

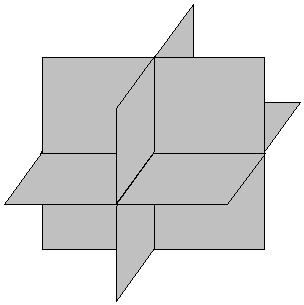
POSICIONES RELATIVAS DE TRES PLANOS

Para estudiar la posición relativa de tres planos nos vamos a centrar en único caso, cuando los planos vienen dados en sus ecuaciones implícitas. Por tanto, sean los planos π: Ax+By+Cz+D=0, π»=A»x+B»y+C»z+D»=0 y π»»=A»»x+B»»y+C»»z+D»»=0, consideraremos el sistema formado por las tres ecuaciones y estudiaremos el rango de la matriz de los coeficientes (A) y el de su matriz ampliada (A|B) para determinar las posiciones relativas.

1. Si rang(A)=rang(A|B)=1, entonces los planos son coincidentes.

2. Si rang(A)=1 y rang(A|B)=2, entonces pueden darse dos casos:

a) Si no hay dos filas que sean proporcionales: los tres planos son paralelos.

b) Si hay una fila que sea proporcional a otra, entonces dos planos son coincidentes y el tercero paralelo.

3. Si rang(A)=rang(A|B)=2, también pueden darse dos casos:

a) Si no hay dos filas proporcionales: los tres planos se cortan en una recta común.

b) Si hay una fila proporcional a otra: dos planos son coincidentes y el tercero corta en una recta.

4. Si rang(A)=2 y rang(A|B)=3, una vez más tenemos dos casos:

a) Si no hay filas proporcionales: los tres planos se cortan dos a dos en tres rectas paralelas entre sí.

b) Si hay una fila proporcional a otra: dos planos son paralelos y el tercero los corta en dos rectas paralelas.

5. Si rang(A)=rang(A|B)=3, entonces se cortan en un punto.