Relaciones de equivalencia

Por último, vamos a ver el último tipo de relaciones binarias que nos quedan, las relaciones de equivalencia. Veremos las propiedades que tienen que cumplir el último tipo y como comprobar que realmente son relaciones de equivalencia. Además veremos dos nuevos conceptos que se obtienen a partir de las relaciones de equivalencia.

DEFINICIÓN

Diremos que una relación binaria es de equivalencia cuando cumple las propiedades reflexiva, simétrica y transitiva.

Ejemplo 1: Dada la relación de equivalencia siguiente: “dos números están relacionados siempre y cuando su diferencia sea un número par” (es decir, aRb ↔ a-b es par), sobre el conjunto de los números enteros; demostrar que es una relación de equivalencia.

Para ello, tenemos que demostrar que se cumplen las cuatro propiedades que hemos mencionado en la definición:

1-Es reflexiva: para todo elemento de los números enteros aRa, ya que a-a=0, que se considera un número par.

2- Es simétrica: para cualesquiera dos elementos de los números enteros, se tiene que si aRb→bRa, ya que si a-b es un número par, entonces b-a también es un número par (aunque con signo distinto). Por ejemplo: 3R5 porque 3-5= -2 (número par), y 5R3 porque 5-3=2 (número par).

3- Es transitiva: Si se cumple que aRb y bRc → aRc, ya que si a-b es un número par y b-c es un número par entonces a-c que también se puede escribir como a-c=a-b+b-c=(a-b)+(b-c) es un número par por ser suma de dos números pares. Por ejemplo: 5R9 (9-5=4 par) y 9R15 (9-15=-6 par), entonces 5R15 (5-15=-10 par).

Ejemplo 2: Comprobar que la relación ser menor que en los números enteros no es una relación de equivalencia.

Es decir tenemos que comprobar que la relación aRb↔a<b cumple las propiedades de la realción de equivalencia.

1- No es reflexiva: aRa↔a<a, lo cual no se cumple.

Ya podríamos decir que la relación no es de equivalencia, pero vamos a comprobar que pasa con el resto de las propiedades.

2- No es simétrica: Ya que si aRb →bnoRa, por ejemplo, 3R7 (3<7) pero 7 no R 3 (7<3 es mentira).

3- Es transitiva: Si aRb y bRc → aRc, ya que si a<b, y b<c, entonces a<b<c.

CONJUNTO COCIENTE Y CLASES DE EQUIVALENCIA

Como podemos deducir a partir de la definición, una relación de equivalencia determina una partición de un conjunto (todos los elementos de un conjunto que estén relacionados pertenecen a la misma parte o subconjunto); análogamente, toda partición de un conjunto permite establecer una relación de equivalencia.

Es decir, una relación de equivalencia divide al conjunto en subconjuntos (o partes) disjuntos los cuales se denominan clases de equivalencia.

Llamamos representante de la clase de equivalencia a cualquier elemento que forme para de la clase [a]={b/aRb}.

El conjunto formado por todas las clases de equivalencia, se denomina conjunto cociente, y se denota por M/R (donde M es el conjunto, y R la relación de equivalencia.

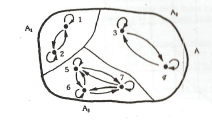
Ejemplo: Dada la siguiente partición y la relación que podemos ver en el diagrama sagital, indicar las clases de equivalencia, un representante de cada clase, y el conjunto cociente.

Las clases de equivalencia con sus respectivos representantes son:

A1=[1]={1,2}

A2=[3]={3,4}

A3=[5]={5,6,7}

El conjunto cociente es: {[1],[3],[5]}.