Relación de orden

Como lo prometido es deuda y a mí me gusta cumplir con mi palabra, vamos a continuar con el artículo de ayer. Vamos a ver dos tipos concretos de relaciones binarias, las relaciones de orden y las relaciones de equivalencia. Hoy empezaremos con las relaciones de orden y además veremos algunos ejemplos en los que demostraremos las propiedades que se cumplen. Y dejaremos para mañana las relaciones de equivalencia… (que intriga, ¿no?)

RELACIONES DE ORDEN

Decimos que una relación binaria es de orden cuando cumple las propiedades reflexiva, antisimétrica y transitiva. Cuando además cumple la propiedad conexa, diremos que el conjunto está totalmente ordenado, en caso contrario diremos que el conjunto está parcialmente ordenado.

Por medio de una relación de orden podemos establecer una ordenación de un conjunto a partir de un criterio. Aunque este criterio no tiene por que ser único. Puede que existan formas diferentes para ordenar el conjunto.

REPRESENTACIÓN DE LAS RELACIONES DE ORDEN

Como mencionamos en el artículo de ayer, todas las relaciones se pueden representar de dos formas, utilizando el diagrama cartesiano o el diagrama sagital.

Cuando representamos una relación de orden mediante el diagrama cartesiano, obtenemos los puntos de la diagonal que divide al eje en dos, puntos de la forma (a,a) y ningún punto para los valores en los que x<y. En cambio con el diagrama sagital cada elemento está relacionado consigo mismo, y las puntas de las flechas solo tienen camino de ida, no de vuelta.

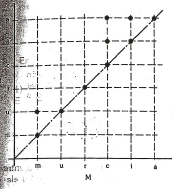
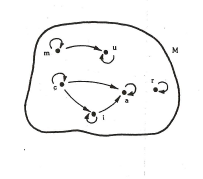
Ejemplo: Representar la relación R definida sobre el conjunto M={m,u,r,c,i,a} mediante el grafo:

R(M)={(m,m), (u,u);(r,r);(c,c);(i,i);(a,a);(m,u);(c,i);(i,a);(c,a)}

Utilizando el diagrama cartesiano:

Y utilizando el diagrama sagital:

Ejemplo: La relación ser múltiplo de sobre el conjunto de los números naturales N, es una relación de orden.

Vamos a comprobar que se cumplen todas las propiedades:

1- Es reflexiva: ya que para todo elemento x, del conjunto N se cumple que xRx. Por ejemplo: 2R2, ya que 2=2∙1.

2- Es antisimétrica: Dados dos elementos cualesquiera se cumple que el uno está relacionado con otro, pero no al contrario: xRy, pero x noR y. Por ejemplo: 4R2, pero 2 noR 4.

3- Es transitiva: Si un número es múltiplo de otro, que a su vez es múltiplo de otro, en entonces el primer número es múltiplo del úlitmo: xRy, e yRz, entonces xRx. Por ejemplo: 18R9, 9R3, entonces 18R3.

4-Pero no se cumple la propiedad conexa, ya que dados dos elementos cualesquiera, estos no tienen por qué estar relacionados. Por ejemplo: si consideramos el 4 y el 5, entonces 4 noR 5, y además 5 noR4.

Luego, la relación ser múltiplo de no es una relación de orden total, por tanto R(N) es un conjunto parcialmente ordenado.

Observación: Si utilizáramos esta misma relación en el conjunto de los números enteros, Z, podemos ver que no cumple la propiedad antisimétrica. Para demostrarlo basta encontrar un ejemplo (o contraejemplo, se llama de esta manera cuando queremos demostrar que algo no es cierto) en el que se cumpla, ya que evidentemente, también habrá ejemplos en los que se cumpla.

Por ejemplo el 1R-1 (ya que 1= 1∙(-1)) pero también se cumple que -1 R 1 (ya que -1= -1∙1).

En este caso, cuando sólo se cumplen las propiedades reflexiva y transitiva de las relaciones binarias, decimos que se trata de una relación de preorden, por tanto, el conjunto R(Z) es un conjunto preordenado.