Relaciones binarias
Llamamos relación binaria a la relación R existente entre dos elementos a y b, de dos conjuntos A y B respectivamente. Indicando que el elemento a está relacionado con b. Esta relación se puede denotar de diversas formas:
1- Como pares ordenados (a, b).
2- Indicando que aRb.
3- Como una mezcla entra los dos anteriores R(a,b).
Al conjunto de todos los elementos relacionados mediante la relación R en un conjunto lo denotamos como R(M)
Está relación dependiendo del conjunto puede referirse a cualquier concepto referido con el conjunto.
Ejemplo: Sea el conjunto A={el conjunto de los números naturales}, una relación binaria del conjunto de A sobre sí mismo puede ser, R= ser múltiplo de.
De tal forma que, por ejemplo 4 está relacionado con 2 (es decir, 4 es un múltiplo de 2), por tanto escribimos 4R2 o (4,2).
En el caso de no estar relacionados escribiremos a no está relacionado con b tachando la R. Un ejemplo de dos elementos que no están relacionados con esta relación son 3 y 5.
Observación: El conjunto R(AxB) de todos los elementos que están relacionados es un subconjunto del producto cartesiano AxB.
FORMAS DE REPRESENTACIÓN
Para representar las relaciones binarias podemos utilizar dos tipos de gráficos:
a) El diagrama cartesiano: donde representaremos los ejes cartesianos, y en cada eje los elementos de cada conjunto. Representaremos las relaciones por medio de puntos ( si el eje es similar al eje de coordenadas) o por medio de cruces si lo representamos mediante cuadrículas.
b) Diagrama sagital o flechas (mediante diagramas de Venn): representaremos los elementos del conjunto dentro del círculo y representaremos las relaciones mediante flechas.
Ejemplo: Representar la siguiente relación:
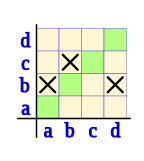
R(M)={(a,b), (b,c), (d,b)}
a) Lo representaremos en primer lugar utilizando el diagrama cartesiano, en este caso utilizando la cuadrícula:
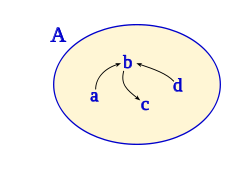
b) Utilizando el diagrama sagital, (la punta de la flecha indica la dirección de la relación):
PROPIEDADES DE LAS RELACIONES BINARIAS
Las relaciones binarias pueden cumplir las siguientes propiedades (no tienen porque cumplir todas, pueden cumplir sólo algunas e incluso ninguna). Dado el conjunto M, y una relación R sobre el conjunto MxM
1. Propiedad reflexiva: Esta propiedad se da cuando todo elemento del conjunto está relacionado consigo mismo: para todo elemento de M x, entonces → xRx.
2. Propiedad simétrica: Dados dos elementos cualesquiera del conjunto M se cumple que si el primer elemento está relacionado con el segundo, entonces se cumple también la relación al contrario, es decir, el segundo está relacionado con el primero: si xRy → yRx.
3. Propiedad antisimétrica: Dados dos elementos del conjunto si el primer elemento está relacionado con el segundo, entonces, el segundo no está relacionado con el primero: si xRy → y noR x.
4. Propiedad transitiva: Dados tres elementos del conjunto, si el primer elemento está relacionado con el segundo, y el segundo relacionado con el tercero, entonces el primero también está relacionado con el tercero: si xRy e yRz → xRz.
5. Propiedad conexa: Dados dos elementos cualesquiera del conjunto estos están relacionados. O bien xRy o bien yRx.
Dependiendo de las propiedades que cumpla una relación determinada, recibe un nombre u otro. Pero esta información la dejaremos para otro días, así como más ejemplos y comprobar estas propiedades.