Aplicaciones matemáticas

Después de estar tres intensos días estudiando los distintos tipos de relaciones que existen entre conjuntos, hoy vamos a estudiar otro tipo diferente relación existente entre dos conjuntos: las funciones o aplicaciones matemáticas. Pero antes de definir el concepto de función, así como sus propiedades, es necesario que introduzcamos el concepto previo de correspondencia.

Una correspondencia entre el conjunto A y B es cualquier operación, ley, norma o criterio que relacione o asocia los elementos de A con los elementos de B. Esta correspondencia la expresaremos con f: A→B.

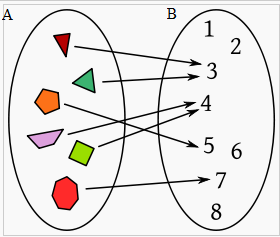
Ejemplo: En la siguiente imagen podemos ver una correspondencia entre los elementos del conjunto A={figuras geométricas} y los elementos del conjunto B={números enteros}, en esta correspondencia a cada elemento de A se le asocia un número del conjunto B, el número de lados.

TIPOS DE CORRESPONDENCIA

Según las relaciones existentes entre los dos conjuntos, las correspondencias se pueden clasificar en distintos tipos:

a) Correspondencia unívoca: cuando a cada elemento del conjunto A le corresponde un único elemento del conjunto B.

b) Correspondencia no unívoca: cuando a uno o más elementos del conjunto A le corresponde más de un elemento del conjunto B.

c) Correspondencia biunívoca: cuando a cada elemento del conjunto A le corresponde un único elemento del conjunto B. Y a cada elemento del conjunto B le corresponde un único elemento del conjunto A.

d) Correspondencia unívoca no biunívoca: cuando a cada elemento de A le corresponde un único elemento de B, pero no a todos los elementos de B le corresponden un único elemento de A.

DEFINICIÓN DE APLICACIÓN MATEMÁTICA

Una aplicación o función es una correspondencia entre dos conjuntos (A y B) de tal forma que a cada elemento de A se le asocia un único elemento de B. Es decir, una función es toda correspondencia unívoca.

Escribimos, f: A→B, de tal forma que si a es un elemento de A, entonces f(a)=b es un elemento de B. Al conjunto de partida lo denominados dominio, y el conjunto final, B; es el conjunto imagen. Por tanto b es la imagen de a.

TIPOS DE APLICACIONES

Según las relaciones existentes entre los elementos de los conjuntos las aplicaciones pueden ser:

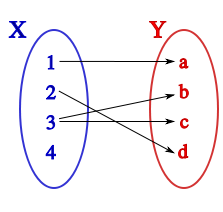
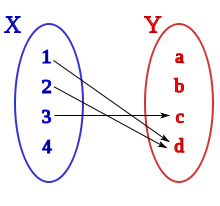
a) Inyectiva: cuando para cada dos elementos del conjunto A: x1 y x2 distintos sus imágenes son distintas, es decir, se cumple que f(x1)≠f(x2).

b) Sobreyectiva (suprayectiva o exhaustiva): Cuando para cada todos los elementos de B existe un elemento en el conjunto A tal que b=f(a). Cuando una aplicación es sobreyectiva, el conjunto imagen coincide con el conjunto B, es decir: f(A)=B.

c) Biyectiva: Cuando se cumple que una aplicación es inyectiva y sobreyectiva a la vez, decimos que la aplicación es inyectiva.