Regla de tres compuesta

La regla de tres compuesta es una forma de resolución de problemas cuyos enunciados están formados por varias reglas de tres simples aplicadas varias veces.

En este caso tendremos dos tipos de reglas de tres: la regla de tres compuesta directa, y la regla de tres compuesta inversa.

a) Regla de tres compuesta inversa.

Para el caso de que sea directa, se resuelve de igual manera que la simple, pero deberemos hacerlo de forma simultánea con las que nos digan en el problema ( tres, cuatro…cinco…).

Eso sí, debemos fijarnos en que las variables son inversamente proporcionales entre sí.

Veamos un ejemplo, utilizaremos otra vez a los famosos obreros de la construcción:

>>Problema:

Un arquitecto de un famoso faraón egipcio está intentando acabar cuanto antes la tumba de su señor, y para ello contrata a 30 trabajadores, los cuales, según sus cálculos, si trabajan 8 horas diarias tardarán 30 días en terminar una parte de la pirámide.

Sin embargo, como el Faraón es un impaciente, le ordena terminar en un plazo mucho menor.

El arquitecto, nervioso, necesita terminar el trabajo inicial en 20 días con los mismos obreros. ¿Cuántas horas deberían trabajar esos empleados para terminar a tiempo?

Primero, como siempre, planteamos el problema:

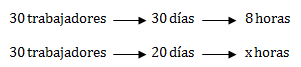
Bien, ya tenemos nuestra incógnita x identificada, por lo que podemos pasar a despejar, teniendo en mente que es una regla de tres inversa por lo que está multiplicando a la x pasa dividiendo y lo demás pasa multiplicando.

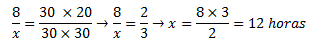
**Pista: Lo que multiplica a la equis sería lo que «la cruza», es decir, el extremo izquierdo de la ecuación. Más sencillo, primero resolvemos la ecuación primera de la izquierda como una regla de tres normal y después igualamos a 8/x.

Entonces, necesitará que sus trabajadores trabajen 12 horas al día para terminar en 20 días el proyecto.

b) Regla de tres compuesta directa

Esta regla de tres se resuelve, al igual que la anterior, teniendo en mente que son varias reglas de tres simples encadenadas.

>>Problema:

En una mina, una cuadrilla de 7 mineros abren una galería de 49 metros de longitud en 21 días. Si otra cuadrilla tiene 14 mineros. ¿Cuántos metros de galerías abrirán en 35 días?

Primero plantaremos el problema, que como observamos, tiene sus magnitudes (mineros, longitud y días) en relación directa, si una aumenta, la otra también aumenta:

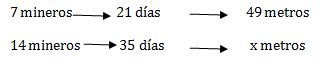
Ahora que tenemos todo planteado, resolvemos la ecuación, en este caso, resolveremos como si fuesen dos ecuaciones simples y después las juntaremos, de forma que:

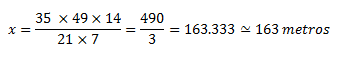
**Pista**: Para resolver el problema, recuerden el producto en cruz, lo que multiplica a la equis pasa dividiendo y a la inversa con lo demás. Solo tienen que agrupar las ecuaciones de dos en dos, de izquierda a derecha.