Regla de Cramer
La regla de Cramer es un teorema que se aplica en álgebra lineal. Es de utilidad cuando se buscan resolver sistemas de ecuaciones lineales. El nombre de este teorema se debe a Gabriel Cramer, que fue quien publicó este método en uno de sus tratados.
Esta regla es aplicada en sistemas que tengan como condición que el número de ecuaciones equivalga al número de incógnitas y que el determinante de la matriz de los coeficientes sea distinto de cero. Si dichas condiciones se cumplen en un sistema, llamaremos a este, sistema de Cramer.
Para calcular este tipo de sistemas en necesario seguir determinados pasos. En primer lugar debemos hallar la matriz ampliada, la cual está asociada al sistema de ecuaciones. Esto quiere decir que la primera columna estará formada por las entradas de los coeficientes de la primera incógnita de las ecuaciones. Por otro lado la segunda columna estará formada por los coeficientes de la segunda incógnita. De esta forma llegaremos a la última de las columnas que estará constituida por las entradas de los términos independientes de las ecuaciones.
Luego de realizado esto podemos proceder a calcular el determinante de A. Aplicamos luego la regla de Cramer que consiste en primer lugar en ir sustituyendo la primera columna del det(A) por los términos independientes. Luego se dividirán los resultados de dicho determinante entre el det (A) para hallar así el valor de la incógnita primera. Si continuamos sustituyendo los términos independientes en las diferentes columnas terminaremos hallando las incógnitas restantes.
La regla de Cramer puede ser una herramienta muy útil para resolver sistemas de ecuaciones lineales, pero es importante tener en cuenta que no es el único método disponible. Existen otros métodos, como el método de eliminación de Gauss o el método de sustitución, que pueden ser más eficientes en ciertos casos. Sin embargo, la regla de Cramer tiene la ventaja de ser un método directo, lo que significa que no requiere de iteraciones para encontrar la solución.
Además, la regla de Cramer también puede ser utilizada para resolver sistemas de ecuaciones no lineales, siempre y cuando se puedan expresar en forma matricial. En este caso, la matriz de coeficientes se convierte en una matriz de Jacobiana, y el proceso para encontrar las incógnitas es el mismo que en el caso de un sistema de ecuaciones lineales.
Veamos a continuación un ejemplo.
Sea el sistema de ecuaciones lineales que se compone de dos ecuaciones con dos incógnitas:
![]()
Hallaremos los valores de x e y, utilizando la regla de Cramer. Comenzaremos este proceso con el primer paso dicho previamente, en el cual debemos hallar la matriz ampliada.
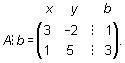
El siguiente paso es el de calcular el determinante de A. Entonces tendremos lo siguiente:
![]()
Finalmente el tercer pasó consiste en calcular las incógnitas.
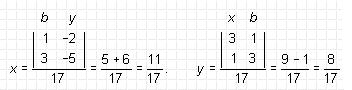
La regla para un sistema de ecuaciones de tres ecuaciones con tres incognitas es semejante pero con una división de determinantes. Veamos un ejemplo:
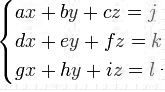
La representación en forma de matriz es la que se muestra a continuación:
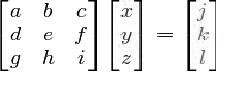
Las incógnitas x,y,z se pueden hallar como se muestra en el siguiente ejemplo:
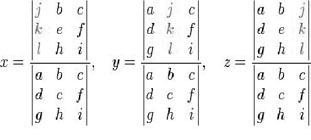
Para sistemas de ecuaciones lineales de más de tres ecuaciones la regla de Cramer resulta enormemente difícil de realizar ya que computacionalmente, es ineficaz para grandes matrices y por esta razón no suele aplicarse cuando de un sistema lineal con muchas ecuaciones se trata.
Es importante mencionar que la regla de Cramer, aunque es un método directo y relativamente sencillo de entender, tiene una limitación importante: su eficiencia computacional. El cálculo de determinantes para matrices grandes puede ser muy costoso en términos de tiempo de cálculo, lo que hace que la regla de Cramer no sea la opción más eficiente para resolver sistemas de ecuaciones con un gran número de incógnitas. En estos casos, se suelen utilizar otros métodos, como la factorización LU o la descomposición QR, que son más eficientes para matrices grandes.
A pesar de esta limitación, la regla de Cramer sigue siendo una herramienta muy útil para la enseñanza del álgebra lineal, ya que proporciona una forma intuitiva y visual de entender cómo se pueden resolver sistemas de ecuaciones. Además, sigue siendo una opción viable para resolver sistemas de ecuaciones de tamaño pequeño a mediano, especialmente en situaciones donde la precisión es más importante que la velocidad de cálculo.
