Método de la regla falsa

El método de la regla falsa, o «falsa posición», es otro de los muchos métodos iterativos para la resolución de problemas con ecuaciones no lineales. La peculiaridad de éste, es que combina dos métodos: el método de bisección y el de la secante (ya explicados en otros artículos).

A continuación veremos una explicación de en qué consiste, y más abajo, os pongo los pasos a desarrollar.

Se basa en trazar una recta que una los extremos de un intervalo dado, considerando que la solución está cerca de uno de éstos extremos.

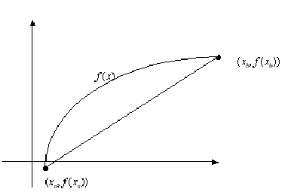
Hemos agregado por tanto, esa línea recta que une el intervalo [a,b]. La idea principal es que si tomamos el punto donde la recta corta el eje x, estaremos más cerca de hallar la raíz.

Entonces, supongamos que tenemos una función f(x), que es continua en el intervalo [xa, xb], y que además f(xa) y f(ba) tienen signos opuestos (RECORDATORIO: Teorema Bolzano) por lo que se deduce que existe al menos una solución para esa ecuación.

Ahora, necesitamos saber la ecuación de la línea recta que une esos dos puntos. Para ello nos ayudamos de la ecuación punto-pendiente, por eso, hallamos la pendiente:

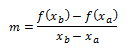
Ahora vamos a sustituir eso en la ecuación de la recta:

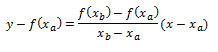
Pero recordamos que la recta en cuestión corta el eje x, así que hacemos y=0:

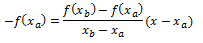
Simplificamos multiplicando todo por xb-xa, para quitar el denominador:

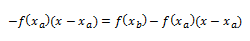
Como paso final, despejamos la incógnita x:

Vamos ahora a describir paso a paso como se desarrolla el método de la regla falsa (considerando f(x) continua):

1) Primero debemos encontrar unos valores iniciales xa y xb tales que:

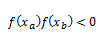
2) Aproximamos a la raíz, para ello usamos:

3) Evaluamos f(xr). Se pueden dar hasta tres casos:

A)

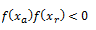
Como f(xa) y f(xr) tienen signos opuestos, por la condición mencionada anteriormente deducimos que, la raíz se encuentra en el intervalo [xa, xr]

B)

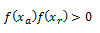
f(xa) y f(xr) tienen el mismo signo. Así que xb y xr han de tener signos distintos, pues:

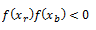
Por tanto, la raíz se encuentra en el intervalo [xr, xa].

*Pista: Como consideramos que la ecuación tiene que ser continua (si o si), al darse este caso, no cumpliría con la condición de continuidad, al menos que tomemos como referencia un tercer punto (xr) cuya imagen (f(xr)) será de signo opuesto.

C)

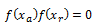
En este caso, como f(xr)=0 ya tenemos localizada la raíz.

 

Debemos repetir estos 3 pasos señalados anteriormente hasta que:

|Ea|<Eb