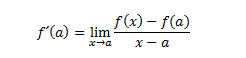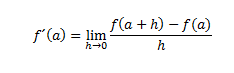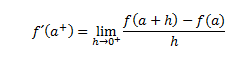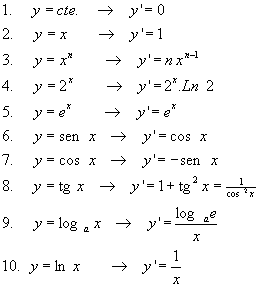Función derivada
DEFINICIÓN
Sea f una función continua definida en un dominio A, se define la función derivada de f en el punto a del conjunto A y se denota por f´(a), al valor del siguiente límite:
Si llamamos h= x-a, también se puede escribir la definición de la siguiente forma:
Si una vez calculada la función derivada, ésta a su vez se puede volver a derivar, esta función se denomina derivada segunda y se denota por f´´. Si nuevamente se puede derivar, se obtendría la derivada tercera y así sucesivamente, conociéndose este proceso por derivadas sucesivas.
Al igual que se han definido los límites por la derecha y por la izquierda, también podemos hablar de derivadas laterales. Llamamos derivada por la izquierda
Análogamente, llamamos derivada por la derecha:
Una función será derivable cuando los límites laterales de la derivada existan y tengan el mismo valor.
INTERPRETACIÓN GEOMÉTRICA
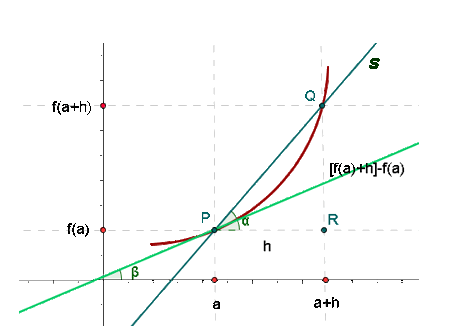
Como podemos observar en la siguiente imagen, la derivada es la pendiente de la recta que une el punto P=(a,f(a)), con el punto Q=(a+h,f(a+h)). Cuando h tiende a cero, los puntos cada vez están más próximos, hasta llegar a confundirse.
Por tanto la derivada de una función en un punto, indica la pendiente de la recta tangente en ese punto.
DERIVADAS MÁS IMPORTANTES
Para poder trabajar con derivadas, en lugar de tener que utilizar la definición que sería más costoso, existen unas reglas (que se pueden comprobar con la definición).
En la siguiente tabla se recogen las derivadas de las funciones elementales.
PROPIEDADES DE LAS DERIVADAS
Sean f y g dos funciones continuas y derivables en su dominio de definición:
1. La derivada de la suma de una función es la suma de sus derivadas: (f+g)´(x)=f´(x)+g´(x)
2. La derivada del producto de dos funciones es igual a la derivada del primer factor por el segundo sin derivar más el primer factor sin derivar por la derivada del segundo: (f•g)(x)=f´(x)g(x)+f(x)g´(x)
3. La derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador sin derivar menos el numerador sin derivar por la derivada del denominar, todo eso dividido entre el denominador al cuadrado: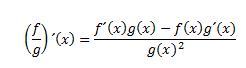
4. La derivada de una función compuesta: f(g(x))=f´(g(x))g´(x)
Hagamos ahora un ejemplo de cada una de las propiedades anteriores:
APLICACIONES
Algunos de los usos más importantes en las matemáticas son:
– Cálculo de la recta tangente en un punto dado, como hemos podido observar en la interpretación geométrica
– Resolver problemas de optimización: minimizar o maximizar funciones de coste, beneficios, etc.
– Estudio de funciones: a partir del estudio de la primera derivada podemos hallar el crecimiento y decrecimiento de una función, así como sus máximos y sus mínimos. Análogamente si estudiamos la segunda derivada podemos hallar la curvatura de la función, los intervalos donde es cóncava o convexa así como sus puntos de inflexión.
– Resolución de límites, mediante la regla de l´Hôpital: cuando nos encontramos con indeterminaciones del tipo 0/0 o ∞/∞, entonces:
Es decir se intercambia el límite del cociente de dos funciones, por el límite del cociente entres sus derivadas. Pudiendo tratarse de límites en un punto finito o en el infinito.