Raíz cuadrada de 2
La raíz cuadrada de 2 es conocida también como constante pitagórica y se denota en general de la siguiente forma:
La raíz cuadrada de 2 equivale a la longitud de la hipotenusa (lado de mayor longitud) de un triángulo rectángulo, sus catetos tienen longitud unidad.
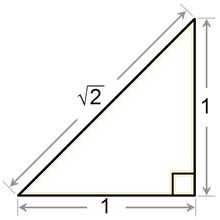
La raíz cuadrada de 2, es un número real positivo que multiplicado por sí mismo da como resultado 2. Fue tal vez el primer número irracional conocido (Un número es irracional si posee infinitas cifras decimales no periódicos, por tanto no se pueden expresar en forma de fracción) Su valor numérico aproximado a 65 posiciones decimales es el siguiente:
1,41421356237309504880168872420969807856967187537694807317667973799
En el área de la geometría la raíz cuadrada de 2 corresponde la longitud de la diagonal de un cuadrado de longitud uno. El valor de la longitud de la diagonal puede ser examinado mediante el Teorema de Pitágoras. Cuando no era tan común el uso de ordenadores (antes de la función SQRT, square root = raíz cuadrada) la aproximación fraccional más próxima era 99/70.
La razón plateada se define de la siguiente forma:
![]()
Las tablas babilónicas del (YBC 7289) (c. 2000–1650 a. C.) otorgan una aproximación de la raíz cuadrada de dos en cuatro dígitos sexagesimales (El sistema sexagesimal es un sistema de numeración posicional que emplea como base la cifra sesenta) que es análogo a seis cifras decimales:
![]()
Otra aproximación antigua a la raíz de dos se da en la antigua India por los textos matemáticos, el Sulbasutras (los textos de sutra forman parte del ritual Śrauta, contienen datos geométricos relacionados con las edificaciones de altares, e incluyen el problema de la cuadratura del círculo). De la siguiente forma:
![]()
El hallazgo de la raíz cuadrada de 2 como un número irracional es atribuido en general al filósofo griego Hipaso de Metaponto. Fue el primero en promover la demostración de la irracionalidad. Se dice que descubrió la irracionalidad de la raíz de 2 cuando intentaba examinar una expresión racional de la misma. No obstante, Pitágoras creía en la definición incondicional de los números como media, y esto le forzaba a no creer en la objetividad de los irracionales. Por esta razón estuvo desde el comienzo en contra de tal manifestación, razón por la cual fue sentenciado a la condena capital por sus asociados pitagóricos.
Para verificar la raíz cuadrada de 2 se debe demostrar que no hay número racional alguno que elevado al cuadrado de cómo resultante 2. Supongamos entonces que tenemos un número racional expresado de forma irreducible, que cumple la ecuación,
![]()
de modo que p si es elevado a 2, resultará par, al ser igual a q elevado a 2 multiplicado por 2. Asimismo si p elevado a 2 es par, p también es par, ya que no existe ningún número impar que tenga como cuadrado un número par.
Veamos ahora si q es impar. Como p es par, se puede escribir p = 2r, donde r corresponde a la mitad de p. Por lo tanto,
![]()
y por el mismo motivo q también debe ser par.
Hay que tener siempre en cuenta que no hay posibilidad de que p y q sean números pares, puesto que entonces la fracción p/q sería reducible (podríamos simplificar el numerador y denominador dividiendo por 2) y comenzamos esta explicación señalando que eran irreducibles.
Además de su importancia en geometría, la raíz cuadrada de 2 tiene una relevancia significativa en otros campos de la matemática y la física. En estadística, por ejemplo, la raíz cuadrada de 2 es la desviación estándar de una distribución normal estándar, que es una de las distribuciones más comunes en estadística. En física, la raíz cuadrada de 2 aparece en la ley de Coulomb, que describe la fuerza entre dos cargas eléctricas.
En la teoría de la probabilidad, la raíz cuadrada de 2 aparece en la fórmula para la densidad de probabilidad de una distribución normal. En la teoría de la información, la raíz cuadrada de 2 es la entropía de una fuente de información que produce dos símbolos con igual probabilidad.
En la teoría de números, la raíz cuadrada de 2 es la base de los logaritmos binarios, que son fundamentales en la teoría de la complejidad computacional. En la teoría de grafos, la raíz cuadrada de 2 es la longitud del camino más corto entre dos nodos en una rejilla cuadrada.
En resumen, la raíz cuadrada de 2 es un número que aparece en una amplia variedad de contextos matemáticos y físicos, lo que refleja su importancia fundamental en estas disciplinas.
