Cálculo de la raíz cuadrada
Uno de los primeros problemas que se enseñan en el colegio, después de las operaciones fundamentales básicas, es el cálculo de la raíz cuadrada. Obviamente, este cálculo lo realizaríamos en caso de que no fuese una raíz inmediata, a saber:
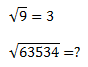
En el primer caso, es obvio que 3×3=9, en el segundo, no es tan simple, debemos realizar una serie de operaciones, que son las que siguen:
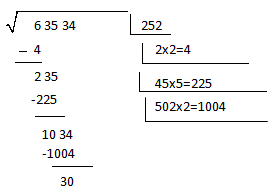
1º) Debemos separar las cifras del radicando (lo que está dentro de la raíz) en grupos de dos, de derecha a izquierda:
2º) Ahora empezamos calculando la raíz cuadrada del primer número, el que está más a la izquierda (en nuestro, caso, el 6):
Debemos pensar, en qué número, elevado al cuadrado, da como resultado 6. Ninguno acude a nuestra mente, sin embargo, el cuadrado de 2 es 4, por lo que se acerca, por tanto, tomaremos éste, colocándolo como vemos a continuación:
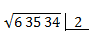
**Nota: Si por ejemplo el numero fuese 8, escogeríamos de entre dos cuadrados, 2 y 3 ( 4 y9 respectivamente) el más pequeño, el dos.
3º) Escribimos a continuación, en el cuadrante que está justo debajo del 2, 2×2=4, y con ese número, debemos restárselo a la primera cifra de la izquierda:
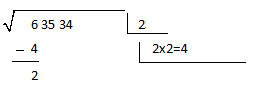
**Pista: Si os fijáis atentamente, os daréis cuenta que se hace casi casi, como las divisiones (si, aquellas que se hacían a mano, sin calculadora, no tanto tiempo atrás).
4º) Bajamos el siguiente par a la derecha del 6, es decir, el 35. Debemos multiplicar por dos el número que ahora mismo está en la parte superior derecha, dándonos 4. Seguidamente añadimos «4_x_=?», los espacios vacios en los guiones, es lo que debemos encontrar. Para ello, simplemente debemos hallar una cifra que nos dé como resultado de esa multiplicación un número menor o igual al que tenemos en la parte izquierda.
Por ejemplo, 46×6=276>235, el 6 no nos valdría, pero el 5 sin embargo sí e acerca a lo que buscamos: 45×5= 225.
No olvidarse de anotar esa cifra que usamos antes (el 5) en la parte superior derecha.
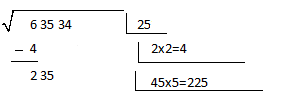
5º) Restamos el número que acabamos de hallar (225) al 235 que tenemos encima. Al lado de el resultado, se baja el último par existente (el 34).
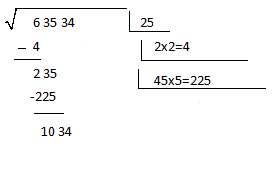
6º) Procedemos igual que antes; primero multiplicamos por dos lo que está en la caja primera (25), dándonos como resultado, 50, y volvemos a replantear 50_x_=?.
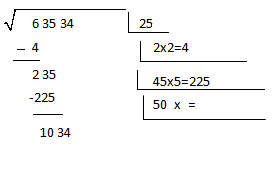
7º) Encontramos que la cifra ideal es 2, con lo que obtenemos 1004, se lo restamos a lo que tenemos en la izquierda, sin olvidarnos de anotar esa cifra que usamos (2) arriba de todo.