Raíz cuadrada de 3
La raíz cuadrada de tres corresponde a un número real positivo que cuando es multiplicado por sí mismo da como resultado el número tres. Se denota de la siguiente forma,
![]()
El valor numérico de la raíz de tres con diez cifras decimales es de 1,7320508075
siendo entonces un número irracional (un número irracional es cualquier número real que no es racional, es decir, es un número que no puede expresarse como fracción, puesto que el decimal sigue para siempre sin repetirse) También se lo puede llamar constante de Teodoro, en honor a Teodoro de Cirene, importante filósofo y matemático griego, nacido en Cirene que hoy en día se conoce como Shahhat, ubicado en Libia. Teodoro de Cirene desarrolló la teoría de los irracionales. Fue alumno de Protágoras y uno de los profesores de Teeteto y Platón.
La raíz cuadrada de 3 es equivalente a la longitud a través de los lados planos de un hexágono regular con los lados de la longitud 1, veamos:
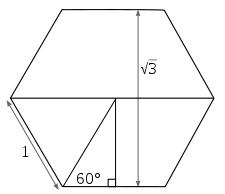
La raíz cuadrada de 3 es igual a la diagonal de un cubo, sus lados miden 1, se puede demostrar esto por el teorema de Pitágoras de la siguiente forma:
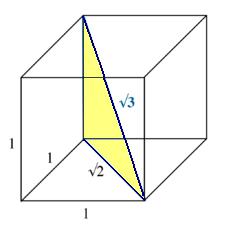
Puesto que las caras que constituyen el cubo tienen como medida 1 podemos proceder a demostrar que la diagonal de cualquiera de sus caras equivale a la raíz cuadrada del número dos.
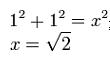
Entonces ahora construyendo un cuadrado el el cual la superficie de este abarque todo el paso de la diagonal del cubo, ese cuadrado tendría unos lados cuyas medidas serían la raíz de 2 y el número 1, siendo la diagonal de este cuadrado la diagonal del cubo, siendo así, al calcular esa diagonal tenemos que:
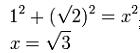
Se demuestra con esto, que la diagonal de un cubo cuyos lados posean la medida uno, será igual a la raíz cuadrada de 3.
La vesica piscis
La vesica piscis (vejiga de pez en latín) o mandorla era un símbolo que se conocía en las antiguas civilizaciones de Mesopotamia, África y Asia. Estaba constituído por dos círculos del mismo radio que se intersecaban de modo que el centro de cada uno de los círculos se encontraba en la circunferencia del otro.
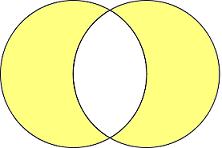
La razón matemática de su anchura (la cual era medida por los puntos de la extremidad del «cuerpo», a excepción de la «cola») multiplicada por su altura fue aproximada por el cociente 265:153. Esta razón, que corresponde a 1,73203, se consideró en la época un número sacro que fué denominado, la medida del pez. Puntualmente, la razón geométrica de estas dimensiones es la raíz cuadrada de 3, o 1,73205… ( puesto que si trazamos la línea recta que une los centros de los dos círculos, junto con los dos puntos donde los círculos se intersecan, se obtiene como resultado dos triángulos equiláteros que se unen por un lado). El cociente 265:153 es solo una cifra aproximada de la raíz cuadrada de 3, no puede obtenerse ninguna aproximación mas justificable con números más pequeños.
