Raíz cuadrada
En matemáticas, se denomina raíz cuadrada √ de un número o raíz, a otro número que debe ser mayor a cero o igual a cero y que si se eleva al cuadrado, será igual al número original. Por ejemplo la raíz cuadrada de x se expresa:
![]()
o bien:
![]()
Por ejemplo:
![]()
La raíz cuadrada es entonces la operación inversa a elevar al cuadrado y consiste en averiguar el número cuando se conoce su cuadrado.
![]()
Para cuadrar un número natural se simplemente multiplica el número por si mismo. O sea, se eleva a la segunda potencia:
![]()
Las raíces cuadradas surgieron ya en la antigüedad siendo el resultado de plantear problemas geométricos como por ejemplo la longitud de la diagonal de un cuadrado. Fueron especialmente investigadas durante el periodo del pitagorismo. El hallazgo de la raíz cuadrada de 2 fué considerado irracional y no conmensurable. Consecutivamente se fue desarrollando la definición de raíz cuadrada. El símbolo de la raíz √fue introducido en 1525 por el matemático Christoph Rudolff. El signo no es más que una forma estilizada de la letra r minúscula para hacerla más elegante, alargándola con un trazo horizontal, hasta adoptar el aspecto usual, el cual representa la palabra latina radix, que quiere decir raíz.
Veamos ahora como calcular la raíz cuadrada de un número.
1. Si el radicando tiene más de dos cifras, debemos separar las cifras en grupos de dos empezando por la derecha.
![]()
2. Luego debemos calcular la raíz cuadrada entera o exacta, del primer grupo de cifras por la izquierda.
¿Qué número elevado al cuadrado nos da 8 como resultado?
8 no es un cuadrado perfecto pero está comprendido entre dos cuadrados perfectos que son: 4 y 9, por lo cual tomaremos la raíz del cuadrado perfecto por defecto: 2, y a continuación lo colocamos en la casilla correspondiente.
![]()
3. El cuadrado de la raíz obtenida se resta al primer grupo de cifras que aparecen en el radicando.

El cuadrado de 2 es 4. Se lo restamos a 8 y obtenemos 4.
4. Detrás del resto debemos colocar el sucesivo grupo de cifras del radicando, separando del número formado la primera cifra a la derecha y dividiendo entonces lo que resta por el duplo de la raíz anterior.

Bajamos 92, siendo la cantidad operable del radicando: 492.
49 : 4 > 9, tomamos como resultado 9.
5. El cociente que se adquiera se colocará detrás del duplo de la raíz, multiplicando el número formado por él, y restándolo a la cantidad operable del radicando.
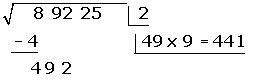
Si hubiésemos obtenido un valor superior a la a la cantidad operable del radicando, habríamos probado por 8, por 7… Hasta de esta forma encontrar un valor mínimo.
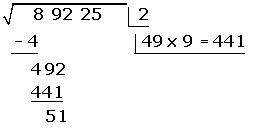
6. El cociente obtenido es la segunda cifra de la raíz.
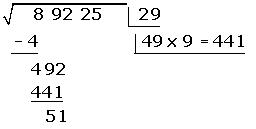
7. Bajamos el siguiente par de cifras y repetimos luego los pasos anteriores.

Como 5301 > 5125, procedemos a probar por 8.
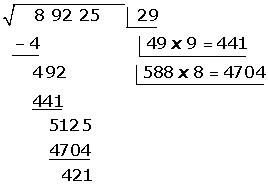
Subimos el 8 a la raíz.
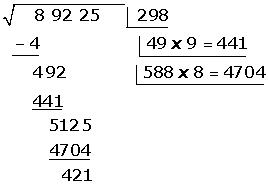
8. Prueba.
Para que el resultado sea correcto, se tiene que cumplir que el radicando es igual a la raíz entera elevado a dos, con la suma del resto.
89 225 = 2982 + 421
